Что такое предикатный глагол

Разница между предикатом и глаголом

Определение

Предикат — это часть предложения, которая содержит глагол и дополнительную информацию о предмете. С другой стороны, глагол является основной частью предиката, который описывает действие, состояние или вхождение.

грамматика

Предикат является фундаментальной частью предложения, поскольку он дополняет предложение, предоставляя глагол, объект и другие дополнения и предложения. С другой стороны, глагол — это слово, которое объясняет действие или состояние субъекта. Таким образом, он должен соответствовать времени предложения, полу и номеру субъекта и т. Д.

Пользы

Предикат имеет важное значение, так как это часть предложения, которая содержит основную информацию о предмете. Точно так же, помимо того, что оно является словом, описывающим действие или состояние субъекта, глагол также выступает в качестве основной части предложения, которое составляет предикат предложения

Заключение

Поскольку глагол является частью предиката в предложении, у большинства людей возникает путаница относительно различий между предикатом и глаголом. Тем не менее, предикат является основной частью предложения, а глагол является основным компонентом в нем. Более того, именно этот пункт (затруднительное положение) содержит глагол, объект и другие дополнения, которые предоставляют информацию о предмете предложения.

В современных теориях синтаксиса и грамматики

Большинство современных теорий синтаксиса и грамматики черпают вдохновение для теории предикатов из логика предикатов как связанный с Готтлоб Фреге. Это понимание рассматривает предикаты как связи или же функции над аргументы. Предикат служит либо для присвоения свойства объекту единичный термин аргумент или связать два или более аргумента друг с другом. Предложения состоят из предикатов и их аргументов (и дополнений) и, таким образом, являются структурами предикат-аргумент, посредством чего данный предикат рассматривается как связывающий его аргументы в большую структуру. Такое понимание предикатов иногда отображает предикат и его аргументы следующим образом:

Это дожди! → дожди ()

Боб смеялись. → засмеялся (Боб) или засмеялся = ƒ (Боб)

Сэм помог ты. → помогло (Сэм, ты)

Джим дал Джилл его собака. → дал (Джим, Джилл, его собака)

Предикаты помещаются слева вне скобок, тогда как аргументы предиката помещаются внутри скобок. Признается валентность предикатов, посредством чего данный предикат может быть авалентным (дожди в первом предложении), одновалентный (смеялись во втором предложении), двухвалентный (помог в третьем предложении), или трехвалентный (дал в четвертом предложении). Эти типы представлений аналогичны формальный семантический анализ, когда речь идет о правильном учете фактов объема логические кванторы и логические операторы. Что касается базовой структуры предложения, однако, эти представления предполагают, прежде всего, что глаголы являются предикатами и именными фразами, которые они появляются вместе со своими аргументами. При таком понимании предложения бинарное разделение предложения на подлежащее NP и предикат VP вряд ли возможно. Вместо этого глагол является сказуемым, а словосочетания существительных — его аргументами.

Другие функциональные слова (например, вспомогательные глаголы, определенные предлоги, фразовые частицы и т. Д.) Рассматриваются как часть сказуемого. В следующих примерах матричные предикаты выделены жирным шрифтом:

Счет будет смеяться.

Будем Счет засмеялись?

Который смешно.

Имеет который было смешно?

Они был удовлетворен.

Имел Oни был доволен, …

Масло в чертежник.

Фред сфотографировал Сью.

Сьюзен тянет ваш нога.

Кому сделал Джим дайте его собака?

Ты должен дать Это вверх.

Обратите внимание, что частью предиката матрицы могут быть не только глаголы, но также прилагательные, существительные, предлоги и т. Д

Понимание предикатов, предлагаемое этими примерами, видит основной предикат предложения, состоящий, по крайней мере, из одного глагола и множества других возможных слов. Слова предиката не обязательно должны образовывать строку или составной элемент, они могут быть прерваны своими аргументами (или дополнениями). Подход к предикатам, проиллюстрированным этими предложениями, широко распространен в Европе, особенно в Германии.

Это современное понимание предикатов совместимо с грамматика зависимостей подход к структуре предложения, который ставит конечный глагол в качестве корня всей структуры, например

Предикат матрицы (снова) отмечен синим, а два его аргумента — зеленым. Хотя предикат не может быть истолкован как составляющая в формальном смысле, это катена. За исключением прерывность, предикаты и их аргументы всегда являются катенами в структурах зависимостей.

Формальное определение

• Точная семантическая интерпретация атомной формулы и атомного предложения будет варьироваться от теории к теории.
• В пропозициональной логике атомные формулы называются пропозициональными переменными. В некотором смысле это предикаты с нулевыми значениями.
• В логике первого порядка атомная формула состоит из предикатного символа, применяемого к соответствующему числу членов.
• В теории множеств предикаты понимаются как характерные функции или задают функции индикатора, т. е. функции от заданного элемента до значения истины.
• Метод построения видов суждений использует предикаты для их определения.
• В автоэпистемической логике, которая отвергает закон исключенного среднего, предикаты могут быть истинными, ложными или просто неизвестными, т. е. данный набор фактов может быть недостаточным для определения истины или ложности предиката.
• В нечеткой логике предикаты являются характерными функциями распределения вероятностей. То есть строгая истинная / ложная оценка предиката заменяется величиной, интерпретируемой как степень правды.

Определение

В логике и лингвистике предикат — это сказуемое суждения, то есть то, что высказано с отрицанием или утверждением о субъекте. Такие слова показывают отсутствие или наличие у предмета того или иного признака. С точки зрения лингвистики, говорится о семантических и синтаксических предикатах. Последний — элемент поверхности структуры, то есть сказуемое, а первый является ядром семантической конфигурации, отображающей ситуацию вне языка, то есть её ядерную семантему.

Таким же образом семантический предикат представляется самыми разными способами и на уровне поверхности структуры. Взаимного однозначного соответствия между этими двумя типами предикатов нет, поскольку любым из них можно отразить одну и ту же ситуацию. Например: я ставлю лапти в угол; я поставила лапти в угол; поставленные в угол лапти. Традиционно не имеющая решения задача языкознания относится к определению понятия предиката. Положительный ответ был бы существенным для развития концепции — семантической или синтаксической, однако предикат пока не получил однозначного определения.

Составляющие

Предикаты составлены по семантическому принципу таким образом: собственно предикаты (например — состояния) и актанты (участники события). Семантически актанты тоже имеют разделение на типы:

• Субъект (иначе — агенс) — это субъектного типа актант или активное действующее лицо. Например: дерево растёт.
• Объект — это адресат прямого или косвенного действия, подвергающийся или нет прямому воздействию. Например: кошка ловит мышку.
• Инстументатив — предмет, без которого ситуация не может осуществиться. Например: наелись супом.
• Результатив — обозначение результата совершённых действий. Например: весной выросла трава.

Кроме того, не обойтись и без сирконстант — обстоятельств совершения действий. Они тоже разделяются на группы. Две самые частые и основные — темпоратив и локатив. Например: весной становится тепло. Слово «весной» — темпоратив. Повсюду расцветает сирень. Слово «повсюду» — локатив.

Кванторные операции над предикатами

Прежде чем изучить квантовые операции, нужно разобраться, что из себя представляет сам квантор.

Квантор — общее название для логических операций, ограничивающих область истинности какого-либо предиката и создающих высказывание.

Кванторы впервые были определены немецким математиком Готлобом Фреге. Он упомянул их в своей работе «Begriffsschrift» («Исчисление понятий», 1879 года). Однако сам термин был изобретен английским логиком Чарльзом Пирсом в 1885 году. Вместе со словом «квантор» он ввел также и термин «квантификация», который означает измерение качеств признаков.

Обозначение кванторов

Символическое обозначение кванторов придумал итальянский математик Дж. Пеано в 90-е годы XIX века. Выглядят эти символы так:

\(\forall\) — «для любого», «для каждого», «для всех»;

\(\exists\) — «существует», «найдётся».

Кроме самих кванторов и вместе с ними используют обозначения \(«!», «:», «|»\), которые являются сокращениями:

! – «единственный»;

– «такой, что»;

| – «такой, что».

Знак «:» обычно используется в формулировках определений или теорем, которые записываются с помощью кванторов. Знак «|» применяется в определениях множеств.

Квантор общности \(\forall\)

Операция связывания квантором общности — это правило, в соответствии с которым каждому одноместному предикату P(x) во множестве N сопоставляется высказывание \((\forall x)(P(x))\), которое произносится, как «для всякого \(x — P(x)\) ».

Оно истинно только в том случае, когда \(P(x)\) — тождественно истинен. В ином случае данное высказывание ложно.

Операция связывания квантором общности по переменной \(x_1\) — это правило, в соответствии с которым каждому n-местному \((n\geqslant2)\) предикату \(P(x, x_2, …, x_n)\), на множествах \(N_1, N_2, …, N_n\),  в соответствие ставится новый \((n-1)\) — местный предикат. Он обозначается как \((\forall x)(P(x, x_2, …, x_n)).\)

Оно истинно только в том случае, когда одноместный предикат \(P(x, a_2, …, a_n)\) на множестве \(N_1\) тождественно истинен. В противном случае оно ложно.

Квантор существования \( \exists\)

Операция связывания квантором существования — это правило, по которому каждому одноместному утверждению \(P(x)\) на множестве N соответствует высказывание \( (\exists)(P(x))\), которое звучит так: « существует \( x\), такое, что \( P(x)\), »).

Это высказывание ложно только, когда \(P(x)\), тождественно ложен. В противном случае оно истинно.

Операция связывания квантором существования по переменной \(x_1\) — это правило, в соответствие с которым каждому n-местному \((n\geqslant2)\) высказыванию \(P(x_1, x_2, …, x_n)\) на множествах \(N_1, N_2, …, N_n\) соответствует новый (n-1-местный предикат. Он обозначается как \((\exists)(P(x_1, x_2, …, x_n)\). Это высказывание ложно только в том случае, если одноместный предикат \((P(x_1, a_2, …, a_n)\) на множестве \(N_1\) тождественно ложен. В противном случае данное высказывание истинно.

Теоретическая часть

Существует много дедуктивных систем для видов суждений и логики первого порядка, которые являются как звуковыми (все доказуемые утверждения верны во всех моделях), так и полными (утверждения, которые верны для всех моделей, являются доказуемыми). Хотя отношение логического следствия разрешимо лишь наполовину, в автоматизированной теореме, доказанной в логике первого порядка, достигнут значительный прогресс. Логика первого порядка также удовлетворяет нескольким металогическим теоремам, которые делают ее пригодной для анализа в теории доказательств, такой как теорема Левенхайма-Сколема и теорема о компактности.

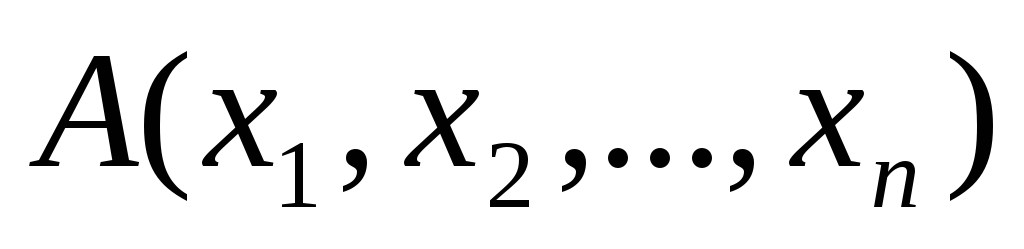
Логика первого порядка является стандартом для формализации математики в аксиомах и изучается в основах математики. Арифметика Пеано и теория множеств Цермело-Френкеля являются аксиоматизациями теории чисел и теории множеств, соответственно, являются частью логики первого порядка. Однако теория первого порядка не имеет возможности однозначно описывать структуру с бесконечной областью, например натуральные числа. Системы аксиом, которые полностью описывают эти две структуры (то есть системы категориальной аксиомы), могут быть получены в более сильных формах логики, таких как логика второго порядка.

Основы логики первого порядка были разработаны независимо Готлобом Фреге и Чарльзом Сандерсом Пирсом.

Кинестетические предикаты

Активный, ароматный, балансировать, баюкать, бежать, бить, благоухать, болеть, бросать, бурлить, варить, весить, взять, вибрировать, вить, вкусный, влечь, водить, волновать, вонючий, вручать, вязать, гибкий, гладить, глотать, гнать, гнуть, головокружительный, горький, горячий, греть, грызть, гулять, давать, давить, двигать, держать, дрожать, дуть, душистый, душный, дымный, дышать, жалить, жать, жевать, жёсткий, задевать, зажимать, зарядить, застрять, затхлый, идти, изможденный, икать, касаться, кидать, кипеть, кислый, класть, колотить, колоть, комфортный, контактировать, корежить, крепить, крутить, крушить, крыть, ласкать, легкий, леденящий, лежать, лепить, лететь, лизать, липкий, ловить, массивный, махать, мокрый, морозный, мягкий, мягкотелый, напористый, напрягать, нежиться, неподвижный, нести, нырять, нюхать, опираться, ослабить, острый, остывать, осязать, отпечатывать, охладеть, ощущать, падать, пахнуть, перчить, питать, плавать, плевать, плести, плотный, поверхностный, поднимать, потеть, преграждать, предвкушать, пресмыкаться, пресный, прогорклый, прокуренный, промозглый, проникнуть, прохлаждаться, прочный, прыгать, пряный, пузыриться, пустой, пушистый, пыхтеть, пышущий, растравить, расщеплять, рвать, резать, свежий, сечь, сжать, сильный, склизкий, скользить, слабый, сладкий, смаковать, смачный, снарядить, сногсшибательный, солить, сочный, спёртый, спотыкаться, стоять, твердый, тёплый, тереть, терпкий, тесный, течь, толкать, тормозить, тошнотворный, трогать, трясти, тугой, тупой, тыкать, тяжелый, ударять, удить, улавливать, упереться, упругий, устойчивый, ухнуть, хапать, хватать, хлестать, ходить, холодный, царапать, целовать, цеплять, чесать, чувствовать, чуять, шевелить, шероховатый, шершавый, шокировать, щекотать, щипать, щупать

Логические операции над предикатами

Так как предикаты принимают два значения, «истина» и «ложь» (1 и 0), к ним можно применить все операции алгебры логики.

Представим, что в неком множестве N определены два предикатаP(x) и Q(x). Рассмотрим все операции с ними по-отдельности.

Конъюнкция — предикат \(P(x)^Q(x)\), приминающий значение «истина» исключительно при значениях \(x\in N\), при которых каждый из предикатов принимает значение «истина», а значение «ложь» принимает во всех остальных случаях. Область истины предиката \(P(x)^Q(x)\) — пересечение областей истинности обоих предикатов: \(I_{P^Q}I_P\cap I_Q.\)

Дизъюнкция двух предикатов — предикат \(P(x)\vee Q(x)\), принимающий значение «ложь» исключительно при значениях, когда каждый предикат принимает значение «ложь». Во всех остальных случаях он принимает значение «истина».

Область истины в этом случае — объединение областей истинности обоих утверждений.

\(I_{P\vee Q}I_P\cap I_Q.\)

Отрицание высказывания P(x) — предикат \(\overline{P(x)}\), принимающий значение «истина» при всех значениях \(x\in N\), когда высказывание P(x) принимает значение «истина».

Область истины здесь — дополнение множества истинности утверждения P(x) до множества N, иначе говоря \(I_overline{P}=N\I_P=CI_P.\)

Импликация — предикат \(P(x)\rightarrow Q(x)\), который остается ложным исключительно при тех значениях \(x\in N\), в которых одновременно P(x) — истинно, а Q(x) — ложно, во всех остальных значениях истинно.

При каждом x справедливо равенство \(P(x)\rightarrow Q(x)=\overline{P(x)}\vee Q(x)\), а это значит, что область истинности \(P(x)\rightarrow Q(x)\) — объединение дополнения области истинности P(x) до множества N и области истинности предиката Q(x). Обозначается выражением: \(I_{P\rightarrow Q}=I_\overline P\cup I_Q.\)

Эквиваленция утверждений \(P(x) и Q(x) — P(x)\leftrightarrow Q(x)\), который делает истинным высказывание при всех \(x\in N\), где одновременно \(P(x)\) и \(Q(x)\) принимают одинаковые значения истинности.

При каждом фиксированном x справедливо равенство \(P(x)\leftrightarrow Q(x)=(\overline P\vee Q)\wedge(P\vee\overline{Q)}\). Это значит, что области истинности утверждения \(P(x)\leftrightarrow Q(x)\) — конъюнкция объединений дополнения области истинности \(P(x)\) до множества N и области истинности \(Q(x)\), а также области истинности \(Q(x)\) до множества N и ОИ \(P(x)7\). Обозначается формулой \(I_{P\leftrightarrow Q}=(I_\overline P\cup I_Q)\cap(I_\overline Q\cup I_P).\)

Рекомендации

1. , п. 53.
2. Деревья избирательных округов, подобные приведенному здесь, которое делит предложение на подлежащее NP и предикатное VP, можно найти в большинстве учебников по синтаксису и грамматике, например , хотя деревья в этих учебниках будут различаться по важным деталям.
3. Примеры теорий, преследующих такое понимание предикатов, см. , п. 96+), , , п. 49), , п. 187), , , п. 54), , п. 43 и далее), , п. 39), , п. 117) Ошибка harvtxt: нет цели: CITEREFFromkin2000 (помощь), , п. 51).
4. Примеры такого использования обозначений см. , п. 259), , п. 241) Ошибка harvtxt: цель отсутствует: CITEREFvan_RiemsdijkWilliams1987 (помощь), , п. 21f).
5. См. Например , п. 17+), , п. 63) Ошибка harvtxt: цель отсутствует: CITEREFBrownMiller1992 (помощь), , стр.14), , п. 98), , п. 39+). Хотя анализы этих лингвистов различаются, они согласны в том, что различные типы служебных слов сгруппированы вместе как часть сказуемого, что означает, что сложные предикаты вполне возможны.
6. Примеры теорий, расширяющих предикат на другие классы слов (помимо глаголов), см. , , п. 34), , п. 30f), , п. 44).
7. То, что многие предикаты не являются составляющими, признается многими, например , п. 50), , п. 14f).
8. Деревья зависимостей, подобные приведенному здесь, можно найти, например, в .
9. Примеры грамматик, в которых используется термин предсказательсм. например , п. 101), , п. 9), , п. 48), и , п. 4f)
10. Ошибка harvtxt: нет цели: CITEREFCarlson1977a (помощь), Ошибка harvtxt: нет цели: CITEREFCarlson1977b (помощь).

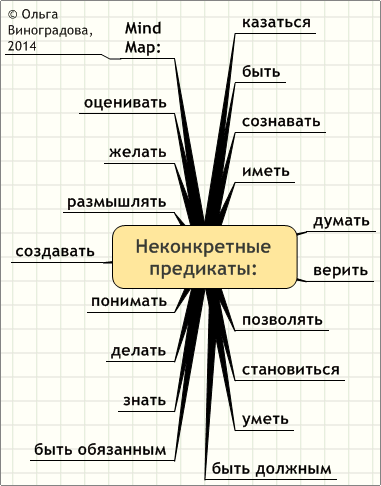
Дигитальные предикаты

Акцентировать, беспокоить, верить, вероятный, веселиться, воспринимать, восхищать, выполнять, вычитать, гадать, глупый, добавлять , догадываться, думать, жить, забывать, загадочный, заканчивать, заслужить, знакомый, знать, изменять, изучать, искать, искренний, использовать, исследовать, ликовать, медитировать, мотивировать, намереваться, находить, начинать, нравиться, обмозговать, обнаруживать, оказываться, осмыслить, осознавать, отказывать, относиться, отправить, оценивать, ошибаться, планировать, подозревать, позволять, помнить, понимать, посещать, постигать, правильный, приветливый, привыкать, придумать, приятный, проверять, происходить, работать, размышлять, расстроить, реагировать, решать, рисковать, слагать, случиться, создавать, сознавать, сокращать, соображать, сосредоточиться, сочетать, спокойный, стоить, стремиться, существовать, считать, таинственный, терпеть, транспортировать, удачный, умирать, умный, успевать, учить, хранить, ценный

Понятие предиката

Утверждения, содержащие в себе переменные, обладающие способностью принимать значения 0 или 1 (ложно или истинно) в зависимости от принимаемых переменными значений, называют предикатами.

В качестве примера может быть рассмотрено выражение x=x^5 представляет собой предикат, поскольку оно будет истинным исключительно в случае принятия переменной x значений 0 или 1 и будет ложным в случае присвоения переменной x всех стальных отличных от 0 и 1 значений.

Множеством истинности Ip любого предиката называют такое множество значений, которое может принимать переменная, позволяющих предикату принимает исключительно истинные значения.

В программировании предикатом принято считать функции, принимающие значения одного или большего числа аргументов и возвращающих значения логического (булевого) типа.

Тождественно-истинным называют предикат, способный принимать истинное значение в случае использования любого набора значений аргумента:

(P(x1,…,xn)=1)

Предикат, для которого использование любого набора значений аргумента приводит к принятию им ложного значения, называют тождественно-ложным:

(P(x1,…,xn)=0)

В случае если предикат приобретает истинное значение при использовании хотя бы одного набора значений аргумента, его считают выполненным.

Поскольку предикаты обладают способностью принимать исключительно значения двух видов – ложно или истинно (0 или 1), к ним могут быть применены все операции, относящиеся к алгебре логики: дизъюнкция, конъюнкция, отрицание и т.п.

Аудиальные предикаты

Акает, аккорд, акцентировать, баритон, басистый, безмолвный, бекать, беседовать, блажить, блеять, болтать, бормотать, бряцать, булькать, визжать, внятный, вокальный, вопить, вопрошать, ворковать, восклицать, вслух, выть, вякнуть, гавкать, гармоничный, гласный, глухой, говорить, гоготать, голосить, гомонить, греметь, громкий, громогласный, грохотать, гудеть, гулкий, диктовать, дискуссировать, диссонирующий, договориться, допрашивать, дребезжать, жужжать, журчать, заикнуться, занудный, заявлять, звать, звенеть, звонить, звонкий, звучать, звякнуть, зычный, игогочет, известить, интервьюировать, интонация, какофония, каркать, квакать, клекотать, кричать, крякать, кукарекать, кукует, кулдыкать, лаять, мекать, мелодичный, многоголосный, молчать, монотонный, мурлыкать, мычать, мямлить, мяукать, настраивать, немой, неразговорчивый, неслыханный, нудить, обсуждать, объявить, оглушительный, озвучить, окает, окликнуть, октава, орать, оркестр, отголосок, отзвук, отрывистый, перекликаться, перефразировать, петь, пищать, повествовать, подпевать, полнозвучный, послушный, потолковать, провозгласить, произнести, пыхтеть, разглашать, разговаривать, разноголосный, раскатистый, рассказывать, реветь, резонировать, речь, ржать, рифма, ругать, рычать, свистеть, симфония, синкопированный, сиплый, сирена, сказать, скрежетать, скрести, скрипеть, скулить, слушать, слышать, собеседник, согласный, созвучный, созывать, сообщить, сопрано, сплетничать, спрашивать, стакатто, стенать, стонать, стрекотать, сюита, тенор, тихий, тон, тональность, трель, трещать, трубить, тугоухий, тявкать, убеждать, уверять, ударение, унисон, упомянуть, урчать, устный, утихнуть, ухать, фыркать, хвалить, хлопать, хриплый, хрустящий, хрюкать, чирикать, членораздельный, шаркать, шелестеть, шептать, шипеть, шорох, шуметь, шуршать, щебетать, щёлкать

Словосочетания: воспринимать на слух, делать замечание, издавать звук, навострил уши, создать звук, увеличить громкость

Предикаторы

Некоторые теории грамматики стремятся избежать путаницы, порожденной конкуренцией между двумя предикатными понятиями, признавая предсказатели. Период, термин предикат используется в традиционном смысле двоичного деления предложения, тогда как термин предсказатель используется для обозначения более современного понимания матричных предикатов. При таком подходе периферийный глагол catenae, кратко проиллюстрированный в предыдущем разделе, являются предикаторами. Далее представлены другие иллюстрации:

Предикторы отмечены синим цветом. Эти глаголы catenae обычно содержат главный глагол и потенциально один или несколько вспомогательные глаголы. Вспомогательные глаголы помогают выразить функциональное значение аспект и голос. Поскольку вспомогательные глаголы несут только функциональную информацию, они не квалифицируются как отдельные предикторы, а скорее каждый раз, когда они образуют матричный предикатор с главным глаголом.

Другая классификация

Можно классифицировать данные слова и на других основаниях. Тип субъекта играет определяющую роль: низшего порядка предикаты относятся к сущностям материальным, а высшего — характеризуют разнообразные виды объектов нематериальных. Здесь резко противопоставляются два вида: относящиеся к событию и характеризующие пропозицию, инвариант. Например: лапти порвались только вчера — лапти порвались, но вчера — очень сомнительно.

Далее, по этой классификации, нужно делить предикаты по количеству актантов. Одноместные: лапти — легки; кедр — мощный; двухместные: лапти легки на ногах; кедр закрыл солнце; трёхместные: лапти легки на ногах при ходьбе; кедр закрыл солнце для подлеска. Другим образом можно разделить предикаты на первопорядковые (непроизводные — кедр стоит); второго порядка (являющиеся производными от первых — кедр стойкий); третьего порядка (производные от вторых) и так далее.

Примеры применения кванторов

Допустим, существует предикат, описывающий отношение «x кратно 7».

Применяя квантор всеобщности, ложные высказывания могут быть записаны следующим образом:

• любое число, являющееся натуральным, делится на 7;
• каждое из чисел, являющихся натуральным, делится на 7;
• все существующие числа, являющиеся натуральными, способны делиться на 7.

Такой квантор будет иметь следующий вид:

( (∀x ∈ N)P(x) )

Применяя квантор существования, истинные высказывания в отношении этого же предиката могут быть записаны следующим образом:

• существуют числа, являющиеся натуральными, которые делятся на число 7;
• может быть найдено натуральное число, кратное числу 7;
• существует хотя бы одно число, являющееся натуральным, способное делиться на число 7.

Запись данного квантора приобретёт вид:

( (∃x ∈ N)P(x) )

Допустим, для множества некоторых простых чисел x образован предикат, описывающий отношение «простое число является числом нечётным». Если перед предикатом вставить слово «любое» получим в результате ложное высказывание, имеющее вид: «любое простое число одновременно является числом нечётным» (число 2, например, будучи числом простым, являясь при этом чётным числом).

Если перед предикатом вставить слово «существует» получим в результате истинное высказывание в виде: «существует простое число, одновременно являющееся нечётным» (x=3, к примеру).

На основании сказанного выше можно заключить, что предикат может быть превращён в высказывание путём присоединения квантора перед ним.

В традиционной грамматике

Предикат в традиционная грамматика вдохновлен логика высказываний античности (в отличие от более современных логика предикатов). Предикат рассматривается как свойство, которым обладает субъект или которым он характеризуется. Следовательно, предикат — это выражение, которое может быть правда о что нибудь. Таким образом, выражение «движется» применимо ко всему, что движется. Это классическое понимание предикатов было более или менее прямо заимствовано в латинских и греческих грамматиках; а оттуда он проник в грамматики английского языка, где применяется непосредственно к анализу структуры предложения. Это также понимание предикатов, как они определены в англоязычных словарях. Предикат — одна из двух основных частей приговор (другой предмет, что предикат изменяет). Предикат должен содержать глагол, и глагол требует или разрешает другим элементам завершать сказуемое, либо запрещает им это делать. Эти элементы объекты (прямой, косвенный, предложный), предикативы, и дополнения:

Она танцы. — Предикат, состоящий только из глагола.

Бен читает книгу. — Предикат глагол-плюс-прямой-объект.

Мать Бена, Фелисити, дал мне подарок. — Предикат глагол-плюс-косвенный-объект-плюс-прямой-объект.

Она слушал радио. — Предикат глагол плюс предложный объект.

Она находится в парке. — Предикат глагол-предикатив-предложная-фраза.

Она встретил его в парке. — Предикат глагол-плюс-прямой-объект-плюс-дополнение.

Предикат предоставляет информацию о субъекте, например, что это за субъект, что субъект делает или каков субъект. Отношение между субъектом и его предикатом иногда называют связь. А предикативный номинал это словосочетание, например, в предложении Георг III — король Англии, фраза король англии являясь предикативным номиналом. Подлежащее и предикативное номинальное должны быть связаны связывая глагол, также называемый связка. А предикативное прилагательное является прилагательное, например, в Ивано привлекательный, привлекательный предикативное прилагательное. Подлежащее и предикативное прилагательное также должны быть связаны связкой.

Это традиционное понимание предикатов имеет конкретный рефлекс во многих структура фразы теории синтаксиса. Эти теории делят английское повествовательное предложение (S) на словосочетание (NP) и фразовый глагол (VP), например

Подлежащее NP показано зеленым, а предикат VP — синим. Эта концепция структуры предложения резко контрастирует с структура зависимости теории грамматики, в которых конечный глагол (т. е. спряженный глагол) как корень всей структуры предложения и, таким образом, отвергнуть это двоичное деление NP-VP, даже для английского языка. Языки с более гибким порядком слов (часто называемые неконфигурационные языки) также часто трактуются по-разному в подходах к построению фраз.

Что такое предикат

Предикат (с латинского praedicatum означает «заявленное, упомянутое, сказанное») — понятие в логике, которым называют утверждение, высказанное о том или ином субъекте. Субъект высказывания — это та вещь или явление, о котором или которой делается утверждение.

Одна из важнейших особенности логики предикатов в том, что все общие имена (такие, как «цветок», «деревня»), знаки свойств («розовый», «большая») и знаки отношений («красивее», «роднее») рассматриваются как относящиеся к одной категории знаков: категории предикаторов (иначе говоря, предметно-истинных функторов).

Предикаторы, в свою очередь, показывают функции, у которых вероятные аргументы — это универсальные в рассмотрении объекты, а значения — истинные оценки. В классической логике они называются «истина» и «ложь». К примеру, возьмем предикатор «человек», который представляет функцию, определяемую как истина каждым отдельным человеком, а каждым отличным от человека существом — как ложь.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Другой пример: функция, которая соответствует предикатору «больше», сопоставляет истину каждой паре объектов или субъектов, один из которых больше. Например, такая пара, как «слон, мышь». Но всем остальным парам, по типу «мышь, слон» и «мышь, мышь», такая функци будет сопоставлять оценку «ложь».

Предикаторы могут быть:

1. Одноместные. Те, которые представляют предметно-истинные функции от одного аргумента. Например, «человек».
2. Двухместные. Те, которым соответствуют функции двух аргументов. Например, «больше».
3. Другие, в зависимости от количества соответствующих аргументов.

Особенности

Этот раздел также можно назвать, или альтернативные заголовки раздела:

Предикаты представляют собой выражения, принимающие значение булевых типов и не определённый тип. Они могут представлять собой как одно выражение, так и любую комбинацию из неограниченного количества
выражений, построенную с помощью булевых операторов AND, OR или NOT. Кроме
того, в этих комбинациях может использоваться SQL-оператор IS, а также круглые скобки для конкретизации порядка выполнения операций.

Предикат в языке SQL может принимать одно из трех значений TRUE (истина), FALSE
(ложь) или UNKNOWN (неизвестно). Исключение составляют следующие предикаты:
NULL (отсутствие значения), EXISTS (существование), UNIQUE (уникальность)
и MATCH (совпадение), которые не могут принимать значение .

Правила комбинирования всех трех истинностных значений легче запомнить, обозначив как 1, как 0 и как 1/2 или 0.5, т.е. половина единицы (где-то между истинным и ложным, т.е. между нулём и единицей).

• с 2-мя истинностными значениями дает минимум этих значений. Напр., = .
• с 2-мя истинностными значениями дает максимум этих значений. Напр., = .
• Отрицание истинностного значения = 1 — данное истинностное значение. Напр., = .

Предикаты сравнения

Предикат сравнения представляет собой два выражения, соединяемых оператором сравнения.
Имеется шесть традиционных операторов сравнения: =, >, <, >=, <=, <> (!=).

• Данные типа (числа) сравниваются в соответствии с их алгебраическим значением.
• Данные типа (символьные строки) сравниваются в соответствии с их алфавитной последовательностью. Если a₁a₂…a_n и b₁b₂…b_n — две последовательности символов, то первая «меньше» второй, если а₁<b₁, или а₁=b₁ и а₂<b₂ и т. д. Считается также, что а₁а₂…а_n<b₁b₂…b_m, если n<m и а₁а₂…а_n=b₁b₂…b_n, т.е. если первая строка является префиксом второй. Напр., ‘folder'<‘for’, т.к. первые две буквы этих строк совпадают, а третья буква строки ‘folder’ предшествует третьей букве строки ‘for’. Также справедливо неравенство ‘bar’ < ‘barber’, поскольку первая строка является префиксом второй.
• Данные типа (дата/время) сравниваются в хронологическом порядке.
• Данные типа (временной интервал) преобразуются в соответствующие типы, а затем

сравниваются как обычные числовые значения типа .

Примеры

Получить информацию о компьютерах, имеющих тактовую частоту процессора не менее 500 МГц и цену ниже $800:

SELECT * FROM Pc
WHERE speed >= 500 AND price < 800;

Запрос возвращает следующие данные:

code	model	speed	ram	hd	cd	price
1	1232	500	64	5	12x	600.0
3	1233	500	64	5	12x	600.0
7	1232	500	32	10	12x	400.0
10	1260	500	32	10	12x	350.0

Получить информацию обо всех принтерах, которые не являются матричными и стоят меньше $300:

SELECT * FROM Printer
WHERE NOT (type = 'matrix') AND price < 300;

Результат выполнения запроса:

Правда или ложь

Если вам все еще непонятно, что такое предикат в математике, то стоит остановиться на этом подробнее. Неформально предикат — это утверждение, которое может быть истинным или ложным в зависимости от значений его переменных. Его можно рассматривать как оператора или функцию, которая возвращает значение, являющееся истинным или ложным. Например, предикаты иногда используются для указания набора элементов: при разговоре о наборах иногда бывает неудобно или невозможно описать набор, перечисляя все его элементы. Таким образом, предикат P (x) будет истинным или ложным, в зависимости от того, принадлежит ли x множеству.