Импеданс элемента
Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.
Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние. Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.
Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где
- Xl — индуктивность;
- Xс — ёмкость;
- R — активная составляющая.
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:
- X > 0, в элементе проявляются индуктивные свойства;
- X = 0, в ёмкости присутствует только активная величина;
- X < 0, в элементе проявляется ёмкостное сопротивление.
Будет интересно Чем отличается пусковой конденсатор от рабочего?
Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.
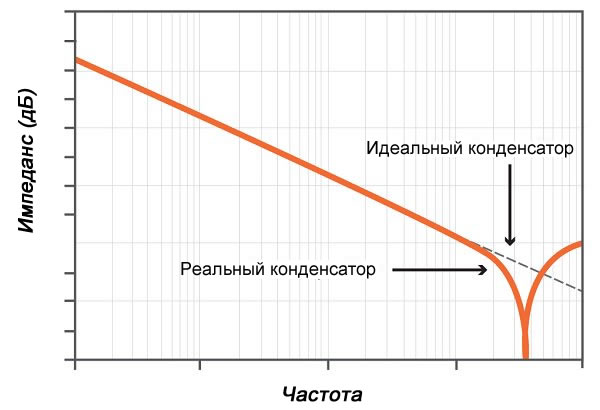
Импеданс элемента.
Какое сопротивление называется реактивным, какое активным
Активное электросопротивление — это важный параметр электрической сети, который обуславливает превращение электрической энергии, поступающей в участок электроцепи или в отдельный элетроэлемент в любой другой тип энергии: химическую, механическую, тепловую, электромагнитную. Процесс превращения при этом считаю необратимым.
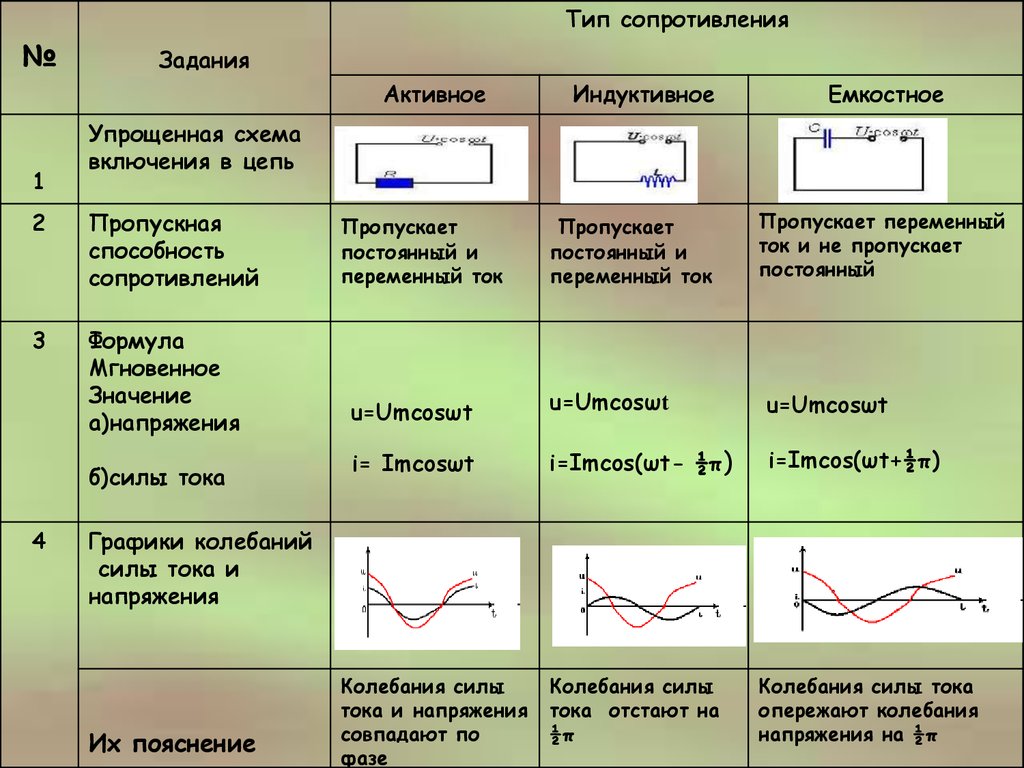
Реактивное сопротивление по-другому называется реактансом и представляет собой сопротивляемость элементов электроцепи, которые вызывается измерением силы электротока или напряжения из-за имеющейся емкости или индуктивности этого элемента. При реактансе происходит обменный процесс между отдельным компонентом сети и источником энергии. Часто это понятие относят к простому электрическому сопротивлению, однако оно отличается некоторыми моментами.
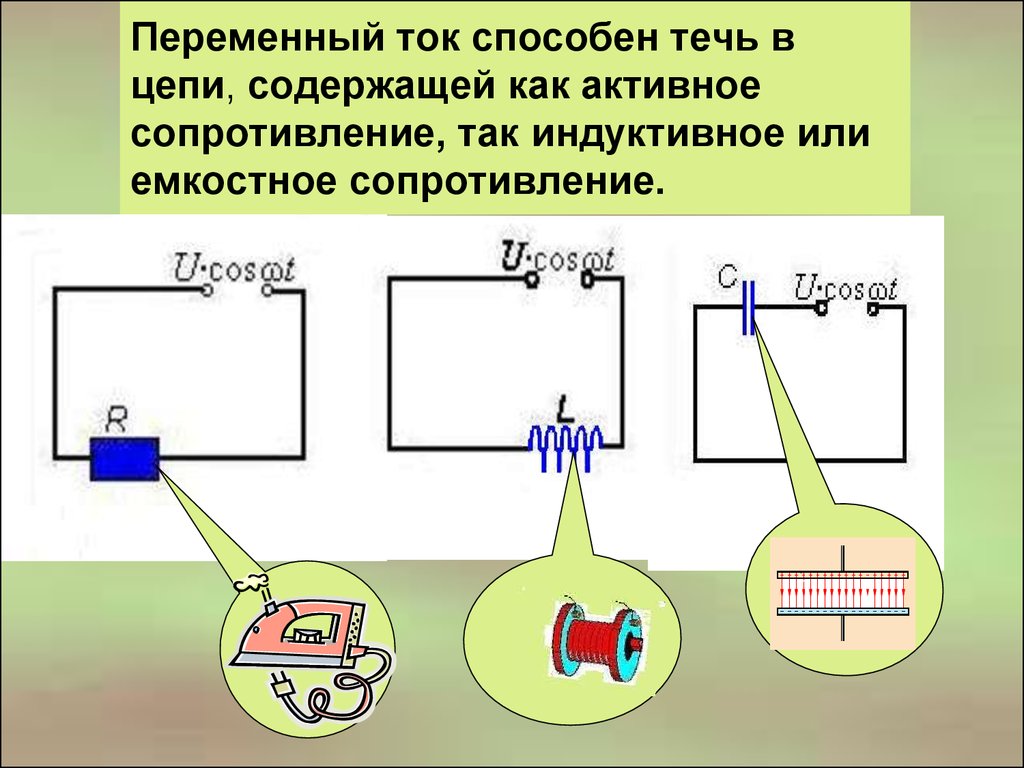
Емкостное сопротивление
В цепи, содержащей емкость и источник переменного тока происходят изменения заряда. Такой емкостью обладают конденсаторы, обладающие максимальной энергией при полном заряде. Напряжение емкости создает сопротивление, противодействующее течению переменного тока, которое считается реактивным. В результате взаимодействия, конденсатор и источник тока постоянно обмениваются энергией.
В конструкцию конденсатора входят токопроводящие пластины в количестве двух и более штук, разделенных слоями диэлектрика. Такое разделение не позволяет постоянному току проходить через конденсатор. Переменный ток может проходить через емкостное устройство, отклоняясь при этом от своей первоначальной величины.

Изменения переменного тока происходят под влиянием емкостного сопротивления. Чтобы лучше понять схему работы, найдем и рассмотрим принцип действия данного явления. Переменное напряжение, приложенное к конденсатору, изменяется в форме синусоиды. Под его воздействием на обкладках наблюдается всплеск, одновременно здесь накапливаются заряды электроэнергии с противоположными знаками. Их общее количество ограничено емкостью устройства и его габаритами. Чем выше емкость устройства, тем больше времени требуется на зарядку.
В момент изменения полупериода колебания, напряжение на обкладках конденсатора меняет свою полярность на противоположное значение, потенциалы также изменяются, а заряды пластин перезаряжаются. За счет этого удается создать течение первичного тока и находить способ противодействовать его прохождению, при уменьшении величины и сдвиге угла. Зарядка обкладок позволяет току, проходящему через конденсатор, опережать напряжение на 90 0 .
Катушка индуктивности в цепи переменного тока
Ну а теперь давайте возьмем катушку индуктивности вместо конденсатора:
Проводим все аналогичные операции, как и с конденсатором. Смотрим на осциллограммы в цепи с катушкой индуктивности:
Если помните, вот такую осциллограмму мы получили в схеме с конденсатором:
Видите разницу? На катушке индуктивности ток отстает от напряжения на 90 градусов, на П/2, или, как еще говорят, на четверть периода (весь период у нас 2П или 360 градусов).
Так-так-так…. Давайте соберемся с мыслями. То есть в цепи с переменным синусоидальным током, ток на конденсаторе опережает напряжение на 90 градусов, а на катушке индуктивности ток отстает от напряжения тоже на 90 градусов? Да, все верно.
Почему на катушке ток отстает от напряжения?
Не будем углубляться в различные физические процессы и формулы, просто сочтем за данность, что сила тока не может резко возрастать на катушке индуктивности. Для этого проведем простой опыт. Так же как и на конденсатор, мы резко подадим напряжение на катушку индуктивности, и посмотрим, что случилось с силой тока.
Как вы видите, при резкой подаче напряжения на катушку, сила тока не стремится также резко возрастать, а возрастает постепенно, если быть точнее, по экспоненте.
Давайте вспомним, как это было у конденсатора:
Все с точностью наоборот! Можно даже сказать, что катушка — это полная противоположность конденсатору ![]()
Ну и напоследок давайте еще побалуемся частотой:
240 Килогерц
34 Килогерца
17 Килогерц
10 Килогерц
Вывод?
С уменьшением частоты сила тока через катушку увеличивается.
Мощность в цепи с реактивными радиоэлементами
Для дальнейшего объяснения этого явления нам потребуется наша осциллограмма с катушки индуктивности:
Итак, давайте выделим на ней один период и разделим его на 4 части, то есть по 90 градусов каждая или π/2.
Давайте начнем с такого понятия, как мощность. Если не забыли, мощность — это сила тока помноженное на напряжение, то есть P=IU. Итак, в первую четвертинку периода t1 у нас напряжение принимает положительные значения и сила тока тоже положительное. Плюс на плюс дает плюс. В эту четверть периода энергия поступает из источника в реактивное сопротивление.
Теперь давайте рассмотрим отрезок времени t2. Здесь ток со знаком «плюс», а напряжение со знаком «минус». В итоге плюс на минус дает минус. Получается мощность со знаком «минус». А разве так бывает? Еще как бывает! В этот промежуток времени реактивный радиоэлемент отдает запасенную энергию обратно в источник напряжения. Для лучшего понимания давайте рассмотрим простой житейский пример.
Представим себе кузнеца за работой:
Не знаю, какое было у вас детство, но я когда был пацаном, брал свинец с аккумуляторов и плющил его в металлические пластинки. И что думаете? Свинец нагревался. Не так, чтобы прям обжигал, а был тепленький на ощупь. То есть моя энергия удара превращалась в тепло, можно даже сказать, в полезную энергию.
А что если взять пружину от стоек ВАЗа и ударять по ней?
С пружиной не станет НИ-ЧЕ-ГО! Она ведь не свинец. Но… заметьте вот такую вещь: как только мы начинаем «плющить» пружину кувалдой, у нас она начинает сжиматься. И вот она сжалась до упора и… выстрелила вверх, подхватив с собой тяжелую кувалду, которая только что пыталась ее расплющить. То есть в данном случае энергия вернулась обратно в источник энергии, то есть обратно к кузнецу. Он вроде как и пытался расплющить пружину, но пружина вернула энергию обратно своим разжатием. То есть кузнецу не надо уже было подымать тяжелый молот, так как за него это уже сделала пружина.
Разжатие пружины и возврат ею энергии обратно — это и есть отрицательная мощность. В этом случае энергия возвращается обратно в источник. Хорошо ли это или плохо — это уже другая история.
В третий промежуток времени t3 и ток и напряжение у нас со знаком «минус». Минус на минус — это плюс. То есть реактивный элемент снова поглощает энергию, ну а на t4, снова ее отдает, так как плюс на минус дает минус.
В результате за весь период у нас суммарное потребление энергии равно чему?
Правильно, нулю!
Так что же это получается тогда? На катушке и конденсаторе не будет выделяться никакой энергии? Получается так. Поэтому в схемах они чаще всего холодные, хотя могут быть и слегка теплыми, так как реальные параметры катушки и конденсатора выглядят совсем по другому.
Эквивалентная схема реальной катушки индуктивности выглядит вот так:
где
RL — это сопротивление потерь. Это могут быть потери в проводах, так как любой провод обладает сопротивлением. Это могут быть потери в диэлектрике, потери в сердечнике и потери на вихревые токи. Как видите, раз есть сопротивление, значит на нем может выделяться мощность, то есть тепло.
L — собственно сама индуктивность катушки
С — межвитковая емкость.
А вот и эквивалентная схема реального конденсатора:
где
r — сопротивление диэлектрика и корпуса между обкладками
С — собственно сама емкость конденсатора
ESI (ESL) — эквивалентная последовательная индуктивность
Здесь мы тоже видим такие параметры, как r и ESR, которые на высоких частотах будут еще лучше себя проявлять, благодаря скин-эффекту. Ну и, соответственно, на них будет выделяться мощность, что приведет к небольшому малозаметному нагреву.
Формула расчета реактивного сопротивления
В общем случае для деталей катушечного типа применяются выражения:
X = L*w = 2* π*f*L.
Для конденсаторов применяют формулы:
X = 1/(w*C)= 1/(2* π*f*C).
Для конкретного элемента, нужные параметры которого известны, величина может быть вычислена с использованием онлайн калькулятора. В форму потребуется ввести нужные данные и нажать на кнопку, инициирующую расчеты.
Умение рассчитывать данную составляющую сопротивляемости поможет узнать величину тепловых потерь на используемых нагрузках. При параллельном подсоединении конденсатора с подходящей емкостью можно решить проблему энергетических потерь на индуктивных нагрузках.
Основные различия между активным и реактивным сопротивлением
Когда электрический ток проходит через элементы с активным сопротивлением, происходят необратимые потери выделяемой мощности. Типичным примером служит электрическая плита, где в процессе работы происходят необратимые превращения электричества в тепловую энергию. То же самое происходит с резистором, в котором тепло выделяется, но обратно в электроэнергию не превращается.
Помимо резисторов, свойствами активного сопротивления обладают приборы освещения, электродвигатели, трансформаторные обмотки, провода и кабели и т.д.
Характерной особенностью элементов с активным сопротивлением являются напряжение и ток, совпадающие по фазе. Рассчитать этот параметр можно по формуле: r = U/I. На показатели активного сопротивления оказывают влияние физические свойства проводника – сечение, длина, материал, температура. Эти качества позволяют различать реактивное и активное сопротивление и применять их на практике.
Реактивное сопротивление возникает в тех случаях, когда переменный ток проходит через так называемые реактивные элементы, обладающие индуктивностью и емкостью. Первое свойство характерно для катушки индуктивности без учета активного сопротивления ее обмотки. В данном случае причиной появления реактивного сопротивления считается ЭДС самоиндукции. В зависимости от частоты тока, при ее возрастании, наблюдается и одновременный рост сопротивления, что отражается в формуле xl = wL.
Реактивное сопротивление конденсатора зависит от емкости. Оно будет уменьшаться при увеличении частоты тока, поэтому данное свойство широко используется в электронике для выполнения регулировочных функций. В этом случае для расчетов используется формула xc = 1/wC.
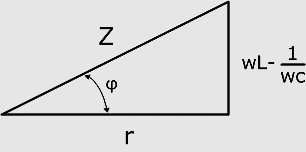
В электронике существует не только активное и реактивное, но и полное сопротивление цепи, представляющее собой сумму квадратов обоих сопротивлений. Этот параметр обозначается символом Z и отображается в виде формулы:
В графике это выражение выглядит в виде треугольника сопротивлений, где реактивное и активное сопротивление соответствуют катетам, а полное сопротивление или импеданс – гипотенузе.
Аналогия с электрическим сопротивлением проводника на примере резистора
Чтобы суметь рассчитать импеданс цепи, нужно представлять, как себя ведут различные входящие в нее элементы: катушки индуктивности, резисторные и емкостные детали, с точки зрения вклада в составляющие общей резистивности цепи.
Активное сопротивление
Резистор относится к числу пассивных деталей цепи, не содержащих внутренних источников электроэнергии, при этом почти все создаваемое им противодействие приходится на активную компоненту. Реактивная составляющая если и присутствует, то настолько мала, что ею зачастую принято пренебрегать. Это связано с тем, что отношение напряжения на деталь и электротока, проходящего через нее, не зависит от их частоты. Когда к резисторной детали присоединяют источник напряжения (обозначим его U), через нее будет идти электроток значением I. Если к концам радиодетали подсоединяют источник тока, равного I, между ними будет иметь место падение напряжения U.
Реактивное сопротивление
К основным компонентам электроцепей, несущим такую нагрузку, относятся дроссели (и подобные им индуктивные элементы) и конденсаторы. При достижении резонанса наблюдается наименьшее значение общего противодействия подключенных последовательно конденсатора и дросселя и наибольшее – включенных параллельно.
Индуктивная нагрузка
Если индуктивный дроссель подключить к постоянному току, на нем будут наблюдаться следующие эффекты: резистивность будет приближаться к нулевому значению, а при пропускании электротока через катушечный элемент падение напряжения будет отсутствовать, независимо от токовой величины:
R=U/I=0/I=0.
Такие цифры справедливы для идеального дросселя, на практике они все же несколько отклоняются от нуля. Если к детали будет приложен переменный ток, напряжение между катушечными выводами будет отличным от нуля.

Катушка индуктивности
Емкостная нагрузка
При включении идеального конденсаторного элемента в сеть с постоянным напряжением его резистивность будет иметь очень большую величину, стремящуюся к бесконечной. Когда к радиодетали прикладывают такое напряжение, проходящий через нее ток будет равен нулю. Если к выводам конденсатора подсоединить источник переменного напряжения, ток будет ненулевым.
Советуем изучить — Измерение электрической энергии

Детали, обладающие емкостью
Данные эффекты, наблюдаемые на емкостных радиодеталях и катушках, нельзя описывать в категориях активного противодействия в условиях константного электротока, так как последнее подразумевает стабильное, независимое от условий и не изменяющееся во времени отношение электротока и напряжения и исключает явление сдвига фаз между этими величинами. Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.
Важно! При рассмотрении поведения катушек и конденсаторов под действием гармонических сигналов обнаруживается, что токовая сила и напряжение могут быть связаны константной величиной, которую также называют импедансом. При ее изучении применяется понятие о гармонических сигналах, учитывающее как их амплитудные характеристики, так и особенности, связанные с фазами. Такое значение импеданса можно определить как частное комплексной амплитуды, которой обладает напряжение приложенного к двухполюсному элементу сигнала, и комплексной амплитуды идущего через элемент электротока
В отношении пассивных электроцепей со стабильными показателями в устоявшемся режиме стоит сказать, что импедансный показатель у них не будет привязанным к течению времени. Если временной параметр при формульной записи не сокращается, то категория импеданса для рассматриваемого двухполюсника окажется неприменимой
Такое значение импеданса можно определить как частное комплексной амплитуды, которой обладает напряжение приложенного к двухполюсному элементу сигнала, и комплексной амплитуды идущего через элемент электротока. В отношении пассивных электроцепей со стабильными показателями в устоявшемся режиме стоит сказать, что импедансный показатель у них не будет привязанным к течению времени. Если временной параметр при формульной записи не сокращается, то категория импеданса для рассматриваемого двухполюсника окажется неприменимой.
Виды пассивных элементов
Внутреннее сопротивление — формула
Данные устройства характеризуются тем, что вместо рассеивания энергии склонны к ее накоплению. Разные типы таких деталей создают различные формы сопротивления.
Катушка индуктивности
Это радиокомпонент, представляющий собой проводниковый элемент спиральной или винтообразной формы, покрытый изоляцией. В схемах катушки используют для нивелирования помех и искажений, снижения величины переменного тока, генерации магнитного поля. Длинные тонкие элементы носят название соленоидов. Катушки отличаются небольшими величинами активной сопротивляемости и емкости, но обладают индуктивностью, генерируя электродвижущую силу.

Подключение катушки в электрическую цепь
Емкостной элемент
Примером этого вида деталей является конденсатор. Он включает в себя две проводящие обкладки, между которыми находится диэлектрический материал. Протекание электротока обусловлено накоплением и отдачей обкладками своего заряда.
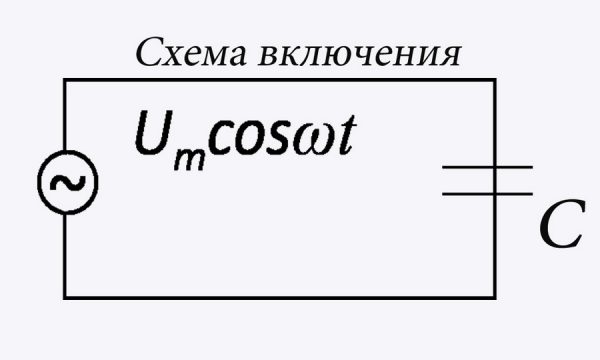
Подсоединение конденсатора в электроцепь
Характеристики реактивного конденсатора
Параметры, характеризующие элементы, наносятся на их внешних корпусах, там же прописываются сведения о типе, наименовании изготовителя и дате выпуска продукции.
Перечень основных критериев:
Номинальная ёмкость – это значение, определенное ГОСТом, задаваемое в диапазоне 0 – 9999 Пф, наносимое на схемы, но без обозначений. Если числа указываются на самом конденсаторе в пределах от 10000 до 9999 в мкФ, то значения надписываются в мкФ (uF).

Единицы
- Далее – наносятся условные отклонения от номинала.
- Еще один важный параметр – показатель номинального напряжения (В). Специалистами рекомендовано использовать в работе элемент с дополнительными ресурсами. Не допускается применять прибор с меньшими показателями, для предотвращения пробоя изоляции из диэлектрического материала, что провоцирует поломку детали.
- Иные характерные параметры на корпусах – рабочая температура, показатель предельной силы тока.
- Количество фаз, от которых осуществляется работа – одна или три.
- По виду установки: внутренняя и наружная.
Вам это будет интересно Как определить сопротивление цепи
Важно! Перечисленные критерии можно увидеть на корпусной детали, а расчет реактивного сопротивления выполнить самостоятельно. Дополнительные характеристики устройства для накопления зарядов:
Дополнительные характеристики устройства для накопления зарядов:
- Удельная ёмкость – это отношение непосредственных габаритов к массе диэлектрического элемента.
- Рабочее напряжение – это номинал, который выдерживает деталь при подаче напряжения на изоляцию.
- Стабильность температуры. В этом диапазоне изменений не отмечается.
- Сопротивление изоляционного слоя. Этот параметр определяется исходя из тока утечки и саморазряда.
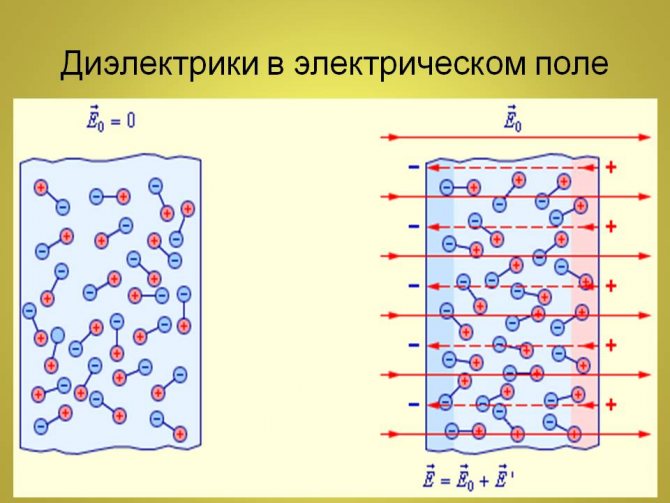
Поле
- Эквивалентное сопротивление – обуславливается потерями на выводах и в диэлектрическом слое.
- Процесс адсорбции. Это разность потенциалов, образовавшаяся на обкатках после обнуления заряда.
- Сопротивление емкости. Возникает при снижении проводимости подачи переменного тока.
- Полярность. При приложении потенциала с соответствующим значением конденсатор функционирует корректно.
- Эквивалентная индуктивность. Это параметр, образующийся на контактах, для возникновения колебательного контура.
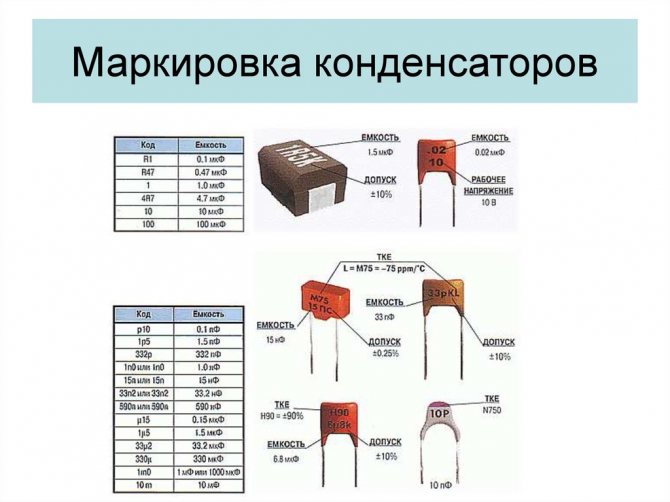
Характеристики
Не совсем яблочко от яблоньки
Лучший способ понять, что же такое полное электрическое сопротивление – это сравнить его с чем-то уже вам известным, скажем – «простым» сопротивлением. Так мы сможем дать исчерпывающее определение полного электрического сопротивления одной фразой:
Вот и всё. Сейчас вы можете остановиться и записать еще одно слово в ваш словарь инженера-электрика. Просто и понятно: полное электрическое сопротивление – вид сопротивления, которое зависит от рабочей частоты электрической цепи. Но, разумеется, это еще не всё.
Резисторы выполняют в цепи постоянного тока чрезвычайно простую работу. Они оказывают сопротивление току, протекающему через какой-либо металл, например медь. Вы добавляете резистор на 220 кОм в цепь постоянного тока, и получаете определенное уменьшение тока, который втекает в резистор с одной стороны, и вытекает из него с другой стороны. Резисторы, подобно другим чисто омическим компонентам электрической цепи, не думают о том, какую же частоту выдает источник тока. Они просто делают то, что должны делать – оказывают некое постоянное сопротивление току.
Но что произойдет, если вы начнете работать с электроникой с питанием от источника переменного тока? Источник переменного тока не просто дает 5 В для питания вашей схемы. Кроме нового источника тока вы получили новые переменные, с которыми необходимо считаться. Например, сюда входит заранее известная частота переменного тока в сети питания. В Соединенных Штатах Америки частота тока в электрической сети составляет 60 колебаний в секунду (60 Гц). За океаном, в Европе, частота тока в сети 50 Гц.
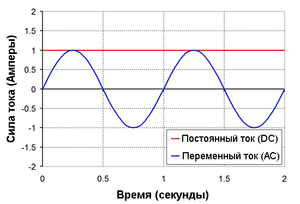
В отличие от постоянного тока (DC), график которого представляет собой
прямую линию, переменный ток (АС) колеблется с определенной частотой.
В итоге получается следующее: в электронных устройствах, использующих переменный ток, необходимы не только активные компоненты, такие как резисторы, задачей которых является оказание сопротивления электрическому току, также нужны компоненты, которые могут реагировать на изменения тока и частоты, например конденсаторы и катушки индуктивности. В противном случае электрическая схема не будет работать так, как задумывалось. Зная все это уже можно посчитать полное сопротивление, которое является старшим братом активного сопротивления. Полное электрическое сопротивление включает в себя и активное, и реактивное сопротивления. Это можно записать в виде выражения:
Индуктивное сопротивление
Реактивное сопротивление подразделяется на два основных вида – индуктивное и емкостное.
При рассмотрении первого варианта следует отметить возникновение в индуктивной обмотке магнитного поля под действием переменного тока. В результате, в ней образуется ЭДС самоиндукции, направленной против движения тока при его росте, и по ходу движения при его уменьшении. Таким образом, при всех изменениях тока и наличии взаимосвязей, ЭДС оказывает на него противоположное действие и приводит к созданию индуктивного сопротивления катушки.

Под влиянием ЭДС самоиндукции энергия магнитного поля обмотки возвращается в электрическую цепь. То есть, между источником питания и обмоткой происходит своеобразный обмен энергией. Это дает основание полагать, что катушка индуктивности обладает реактивным сопротивлением.
В качестве типичного примера можно рассмотреть действие реактивного сопротивления в трансформаторе. Данное устройство имеет общий магнитопровод, с расположенными на нем двумя обмотками или более, имеющими общую зависимость. На одну из них поступает электроэнергия из внешнего источника, а из другой выходит уже трансформированный ток.
Под действием первичного тока, проходящего по катушке, в магнитопроводе и вокруг него происходит наведение магнитного потока. В результате пересечения витков вторичной обмотки, в ней формируется вторичный ток. При невозможности создания идеальной конструкции трансформатора, магнитный поток будет частично уходить в окружающую среду, что приведет к возникновению потерь. От них зависит величина реактивного сопротивления рассеяния, которая совместно с активной составляющей образуют комплексное сопротивление, называемое электрическим импедансом трансформатора.
Особенности активного сопротивления
Сопротивление в электротехнике является важнейшим параметром, с помощью которого какая-то часть электрической цепи оказывает противодействие проходящему по ней току. Образованию данной величины способствуют изменения электроэнергии и ее переход в другие виды энергетических состояний.
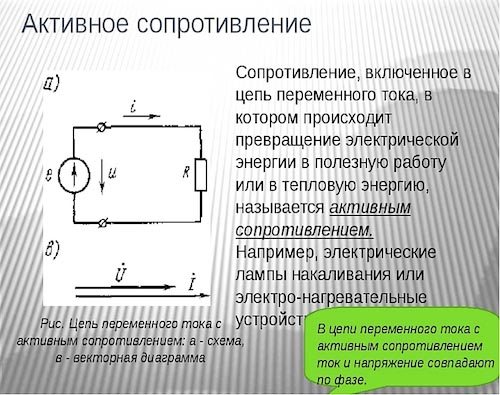
Подобное явление характерно лишь для переменного тока, под действием которого образуются активные и реактивные сопротивления кабелей. Этот процесс представляет собой необратимые изменения энергии или передачу и распределение ее между отдельными элементами цепи. Если изменения электроэнергии принимают необратимый характер, то такое сопротивление будет активным, а если имеют место обменные процессы, оно становится реактивным. Например, электрическая плита выделяет тепло, которое обратно в электрическую энергию уже не превращается.
Данное явление в полной мере затрагивает любые виды провода и кабеля. При одинаковых условиях, они будут по-разному сопротивляться прохождению постоянного и переменного тока. Подобная ситуация возникает из-за неравномерного распределения переменного тока по сечению проводника, в результате чего образуется так называемый поверхностный эффект.
Мощность в цепи с реактивными радиоэлементами
При подключении таких элементов в цепь в четных четвертях периода мощность будет иметь отрицательное значение (в это время компонент направляет накопленную энергию в источник напряжения). В итоге использование энергии элементом за весь цикл оказывается равным нулю. Это означает, что на нем не происходит выделения энергии, так что на электросхемах такие детали изображаются холодными. На деле положение вещей может быть немного иным (это зависит от параметров конкретного элемента), бывает, что небольшие тепловые потери на конденсаторе или соленоиде все-таки имеют место. Но они не будут значительными, измеряющимися в кв.
Как рассчитать Xc
Сила тока цепи с постоянными показателями напряжения в момент работы электроконденсатора равно 0. Ее значения в цепи с переменным напряжением после подключения конденсатора I ? 0. В итоге, цепочке с непостоянным напряжением конденсатор придает Xc меньшее, чем цепочке с неизменным показателем напряжения.
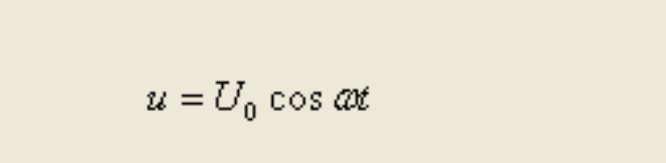
Формула вычисления показателя напряжения за одну секунду
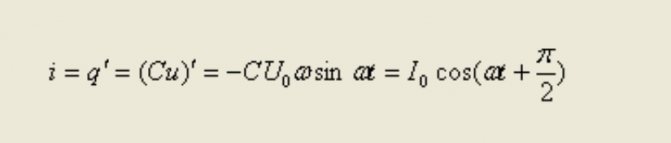
Формула расчета величины силы электротока за мгновение
Получается, что изменения напряжения отличаются по фазе от изменений тока на π/2.
По закону, сформулированному Омом, показатели силы электротока находятся в прямой пропорциональной зависимости от величины напряжения цепи. Формула вычисления наибольших величин напряженности и силы тока:
Вам это будет интересно Особенности светового потока
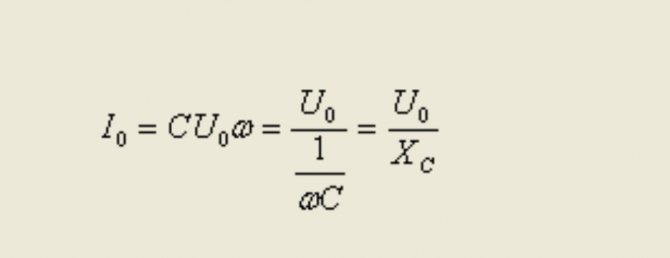
Наибольшие величины напряженности и силы тока можно рассчитывать по формуле
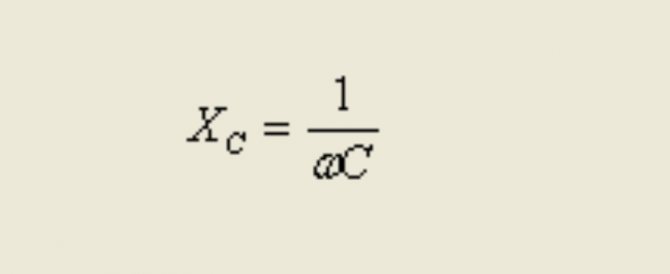
Окончательная формула расчета емкостного сопротивления в цепи переменного тока
ω = 2πf.
f — показатель частоты непостоянного тока, измеряется в герцах;
ω — показатель угловой частоты тока;
С — размер конденсатора в фарадах.
Важно! Xc не выступает параметром проводника, оно находится в зависимости от такой характеристики электроцепи, как частота электротока. Повышение значений данной величины вызывает рост пропускающей способности конденсатора (предел его сопротивления току непостоянному понижается)
Повышение значений данной величины вызывает рост пропускающей способности конденсатора (предел его сопротивления току непостоянному понижается).
Представим, к цепи подключен конденсатор, емкостью 1 мкФ. Необходимо вычислить, уровень емкостного сопротивления при величине частоты 50 Гц и как изменится емкостное сопротивление цепи переменного тока при частоте 1 кГц. Амплитуда напряжения, подведенного к конденсатору, составляет 50 В.
После введения данных в формулу, определяющую Xc, и получаются значения:
Результат для частоты 50 Гц Результат для 1 кГц
Емкостное сопротивление приравнивается к соотношению отклонений колебаний напряжения зажимов электрической цепочки с емкостными параметрами (с небольшими индуктивным и активным сопротивлениями) к колебаниям электротока цепочки. Она равнозначна электроконденсатору.






























