Основные формы мышления в психологии: суждение, умозаключение и понятие

Формулы логики высказываний

Понятие логической формы сложного высказывания уточняется с помощью понятия формулы
логики высказываний.

В примерах 1 и 2 мы учились записывать с помощью логических операций сложные высказывания.
Вообще-то они называются формулами логики высказываний.

Для обозначения высказываний, как и упомянутом примере, будем продолжать использовать буквы

Эти буквы будут играть роль переменных, принимающих в качестве значений истинностные
значения «истина» и «ложь». Эти переменные называются также пропозициональными переменными. Мы будем далее
называть их элементарными формулами или атомами.

Для построения формул логики высказываний кроме указанных выше букв используются знаки
логических операций

~, ∧, ∨, →, ,

а также символы, обеспечивающие возможность однозначного прочтения формул — левая и
правая скобки.

Понятие формулы логики высказываний определим следуюшим
образом:

1) элементарные формулы (атомы) являются формулами логики высказываний;

2) если и —
формулы логики высказываний, то , ,
, ,
тоже являются формулами логики
высказываний;

3) только те выражения являются формулами логики высказываний, для которых это
следует из 1) и 2).

Определение формулы логики высказываний содержит перечисление правил образования
этих формул. Согласно определению, всякая формула логики высказываний либо есть атом, либо образуется
из атомов в результате последовательного применения правила 2).

Пример 6. Пусть — одиночное
высказывание (атом) «Все рациональные числа являются действительными», —
«Некоторые действительные числа — рациональные числа», —
«некоторые рациональные числа являются действительными». Переведите в форму словесных высказываний
следующие формулы логики высказываний:

1) ;

2) ;

3) ;

4) ;

5) ;

6) .

Решение.

1) «нет действительных чисел, которые являются рациональными»;

2) «если не все рациональные числа являются действительными, то нет рациональных чисел, являющихся действительными»;

3) «если все рациональные числа являются действительными, то некоторые действительные числа — рациональные числа и некоторые рациональные числа являются действительными»;

4) «все действительные числа — рациональные числа и некоторые действительные числа — рациональные числа и некоторые рациональные числа являются действительными числами»;

5) «все рациональные числа являются действительными тогда и только тогда, когда не имеет место быть, что не все рациональные числа являются действительными»;

6) «не имеет места быть, что не имеет место быть, что не все рациональные числа являются действительными и нет действительных чисел, которые являются рациональными или нет рациональных чисел, которые являются действительными».

Пример 7. Составьте таблицу истинности для формулы
логики высказываний , которую в
таблице можно обозначить .

Решение. Составление таблицы истинности начинаем с записи значений («истина» или «ложь»)
для одиночных высказываний (атомов) , и
. Все возможные значения записываются в восемь строк таблицы. Далее,
определяя значения операции импликации, и продвигаясь вправо по таблице, помним, что значение равно «лжи» тогда, когда из «истины» следует «ложь».

И	И	И	И	И	И	И	И
И	И	Л	И	И	И	Л	И
И	Л	И	И	Л	Л	Л	Л
И	Л	Л	И	Л	Л	И	И
Л	И	И	Л	И	Л	И	И
Л	И	Л	Л	И	Л	И	Л
Л	Л	И	И	И	И	И	И
Л	Л	Л	И	И	И	Л	И

Заметим, что никакой атом не имеет вида
, ,
, ,
. Такой вид имеют сложные формулы.

Число скобок в формулах логики высказываний можно уменьшить, если принять, что

1) в сложной формуле будем опускать внешнюю пару скобок;

2) упорядочим знаки логических операций «по старшинству»:

, →, ∨, ∧, ~ .

В этом списке знак имеет самую большую область действия, а знак ~ — самую
маленькую. Под областью действия знака операции понимаются те части формулы логики высказываний, к которым
применяется (на которые действует) рассматриваемое вхождение этого знака. Таким образом, можно опускать
во всякой формуле те пары скобок, которые можно восстановить, учитывая «порядок старшинства». А при
восстановлении скобок сначала расставляются все скобки, относящиеся ко всем вхождениям знака ~ (при
этом мы продвигаемся слева направо), затем ко всем вхождениям знака ∧ и так далее.

Пример 8. Восстановите скобки в формуле логики высказываний
.

Решение. Скобки восстанавливаются пошагово следующим образом:

Не всякая формула логики высказываний может быть записана без скобок. Например, в
формулах и
дальнейшее исключение скобок
невозможно.

• Пригодится: минимизация логических функций — общие сведения
• Пригодится: минимизация логических функций методом непосредственных преобразований
• Пригодится: минимизация логических функций методом Квайна

Что такое логика?

Логика – это наука о формах, приёмах и операциях мышления, позволяющих устанавливать или опровергать истинность определенных утверждений, исходя из заведомо известных фактов. Сложно сказать точно, когда она возникла. Отдельные элементы логики присутствуют в работах древнегреческих, древнекитайских и древнеиндийских мыслителей 6-5 веков до н. э., но первым её основные принципы сформулировал Аристотель в 4 веке до н. э.

Изначально она возникла как направление в философии, но со временем развилась в сложную систему знаний и стала самостоятельной научной дисциплиной – формальной логикой. От остальных наук, изучающих мышление, она отличается тем, что абстрагируется от содержания размышлений и высказываний, а изучает их структуру и внутренние закономерности.

Термин «логика» образован от греческого слова λόγος (логос – мысль, слово, причина). Сегодня у него есть два основных значения. Им может обозначаться как научная дисциплина, изучающая закономерности мыслительных процессов и логических построений, так и совокупность правил, которых необходимо придерживаться при построении непротиворечивых умозаключений.

По аналогии

Есть еще один вид умозаключений, который активно используется в человеческом мышлении и речи. Это умозаключение по аналогии. Что это такое? Умозаключение по аналогии — это такое утверждение, при котором несколько предпосылок имеют одну общую черту, на основе которой делается вывод. Это очень интересное и часто непосредственное умозаключение. Примеры можно привести следующие:

• «Айфон — мобильный телефон. И вот этот красненький также является им». В данном случае можно расширить данное умозаключение на такое: «Айфон умеет звонить. Красненький прибор тоже умеет звонить. Айфон — телефон. Он должен уметь звонить. Следовательно, красненький прибор является телефоном».
• «Школьная программа предусматривает изучение в октябре темы дифференциалов. Моя школа изучает дифференциалы. Следовательно, в соседней также изучаются дифференциалы».

В первом примере в качестве общего признака приводится возможность звонить. Во втором же наличие определенной темы в школьной программе. Возможно, примеры не самые точные, но при этом наглядные для большинства людей.

Законы логики

Существует 4 закона, знание которых позволяет лучше понять, что такое логика. Придерживаясь этих законов, можно гарантированно делать правильные и логичные умозаключения при условии наличия достаточного количества точно установленных фактов:

1. Закон тождества

Суть данного закона состоит в том, что суждение сохраняет своё предметное и смысловое значение в рамках одного контекста (например, в пределах одного логического рассуждения). Иными словами, недопустимо в процессе размышления подменять одно значение понятия или суждения другим, поскольку это приведёт к ложному выводу.

К примеру, утверждение «Выучить новый язык можно, общаясь с носителями на житейские темы» истинно в отношение английского или испанского языка, но слабо применимо к языкам программирования. Подобная подмена понятий является одним из грубых нарушений закона тождества. В данном примере она очевидна, но в некоторых случаях она используется как успешный демагогический приём.

2. Закон непротиворечия

Этот закон (называемый также «законом противоречия») гласит, что два высказывания, противоречащих друг другу, не могут быть истинными одновременно. Как минимум одно из них ложно. К примеру, если на столе лежит шар, полностью выкрашенный в один цвет, утверждения «Этот шар белый» и «Этот шар чёрный» не могут быть истинными одновременно. Но они оба вполне могут быть ложными, если шар, к примеру, красный.

Есть три основных типа логических противоречий:

1. Контактные. Это два несовместимых логических высказывания, следующих друг за другом.
2. Дистантные. Это взаимоисключающие высказывания, разделенные определенным интервалом.
3. Мнимые. Это кажущиеся противоречия, которых на самом деле нет, если понимать контекст, в котором делается утверждение (например, «Это красная смородина. А жёлтая она, потому что ещё зелёная»).

Контактные противоречия обычно не пытаются скрыть. Их используют сознательно, чтобы смягчить негативное высказывание («Ты хорошо справился, но это не совсем то, о чём я просил») или, наоборот, усилить его («Отлично! Ты опять всё испортил!»). Дистантные противоречия могут применять демагоги, чтобы запутать собеседника, но чаще их используют по ошибке неопытные или плохо подготовившиеся ораторы.

3. Закон исключённого третьего

Если одно суждение отрицает другое, то одно из них является ложным, а второе – истинным

Здесь важно не путать, что подразумевается под отрицанием

К примеру, утверждения «Этот шар белый» и «Этот шар чёрный» являются всего лишь взаимоисключающими. А отрицающими друг друга являются утверждения «Этот шар белый» и «Этот шар не белый» (одно из них обязательно является истинным, какого бы цвета ни был шар).

4. Закон достаточного основания

Этот закон ввёл Готфрид Лейбниц. Его суть состоит в том, что для того, чтобы считать утверждение истинным, необходимо располагать однозначными доказательствами, исключающими другие варианты. В повседневной жизни люди пренебрегают этим законом логики чаще, чем любым другим, делая однозначные выводы по косвенным фактам.

К примеру, если в середине лета вы несколько дней подряд не видели соседа, которого обычно встречаете ежедневно, можно предположить, что он уехал в отпуск. Скорее всего, так и есть, но всё же этот вывод противоречит закону достаточного основания, поскольку нельзя исключать, к примеру, болезнь или командировку.

Что такое бозоны и элементарные частицы?

Бозоны — это частицы, которые переносят взаимодействие между другими частицами, таким образом, любое притяжение или отталкивание между частицами происходит за счёт того, что они обмениваются бозонами.

Бозон Хиггса был последней частицей открытой в Стандартной Модели. Это критический компонент теории. Его открытие помогло подтвердить механизм того, как фундаментальные частицы приобретают массу. Эти фундаментальные частицы в Стандартной Модели являются кварками, лептонами и частицами-переносчиками силы.

Существует несколько разновидностей бозонов. Так к примеру широко известный фотон является переносчиком электромагнитного взаимодействия, глюон — сильного взаимодействия, а W- и Z-бозоны — слабого взаимодействия.

Согласно современным представлениям бозоны не должны иметь инертной массы, однако, W- и Z-бозоны ею обладают. Для объяснения этого явления британский физик Питер Хиггс постулировал существование некоего поля, получившего впоследствии его имя, из-за взаимодействия с которым W- и Z-бозоны приобретают инертную массу.

Это можно сравнить с пенопластовыми шариками, рассыпанными на поверхности стола, достаточно лёгкого дуновения ветра и их сметёт, а вот если рассыпать их на поверхность воды, то их движение будет замедленно, для W- и Z-бозонов роль воды выполняет поле Хиггса.

Квантами этого поля являются бозоны Хиггса, причём их может быть несколько видов и именно через них происходит взаимодействие поля с W- и Z- бозонами. На основе этого предположения были разработаны различные модели, описывающий этот бозон, но ни одна из них не могла предсказать его энергию.

В связи с этим поиски бозона Хиггса очень затянулись, учёным пришлось буквально перебирать все возможные варианты. Параллельно развивались модели без бозона Хиггса и между сторонниками двух подходов шли жаркие споры. Наконец в 2012 году на Большом Адронном Коллайдере был обнаружен первый кандидат в бозоны Хиггса с энергией 126 ГэВ, а в 2013 появились сообщения подтверждающие, что это действительно бозон Хиггса.

Теория 1964-го года

В 1964 году шестеро физиков-теоретиков выдвинули гипотезу существования нового поля (подобно электромагнитному), которым заполнено все пространство и решает критическую проблему в нашем понимании вселенной.

Независимо от этого другие физики построили теорию фундаментальных частиц, названную в итоге «Стандартной Моделью», которая обеспечивала феноменальную точность (экспериментальная точность некоторых частей Стандартной Модели достигает 1 к 10 миллиардам. Это равнозначно предсказанию расстояния между Нью-Йорком и Сан-Франциско с точностью около 0.4 мм). Эти усилия оказались тесно взаимосвязаны.

Стандартная Модель нуждалась в механизме приобретения частицами массы. Полевую теорию разработали Питер Хиггс, Роберт Браут, Франсуа Энглер, Джералд Гуралник, Карл Хаген и Томас Киббл.

Какова масса бозона?

К несчастью, теория, предсказывающая бозон, не уточняла его массу. Прошли годы, пока не стало ясно, что бозон Хиггса должен быть экстремально тяжелым и, скорее всего, за пределами досягаемости для установок, построенных до Большого Адронного Коллайдера (БАК).

Помните, что согласно E=mc2, чем больше масса частицы, тем больше энергии надо для ее создания.

В то время, когда БАК начал сбор данных в 2010, эксперименты на других ускорителях показали, что масса бозона Хиггса должна быть больше, чем 115 ГэВ/с2. В ходе опытов на БАК планировалось искать доказательства бозона в интервале масс 115-600 ГэВ/с2 или даже выше, чем 1000 ГэВ/с2.

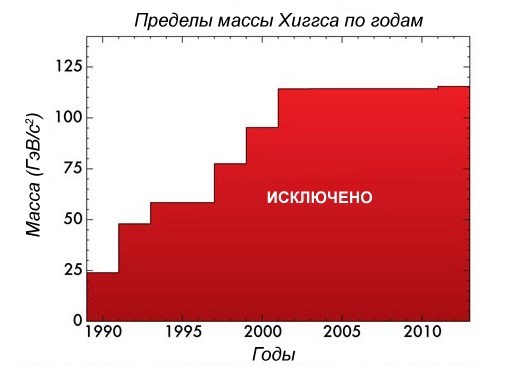
Каждый год экспериментально удавалось исключать бозоны с бОльшими массами. В 1990 было известно, что искомая масса должна быть больше 25 ГэВ/с2, а в 2003 выяснилось, что больше 115 ГэВ/с2.

Дедукция

Только что было сказано, что дедукция характеризуется наличием строгого логического следования между посылками и заключением. Что это означает? Прежде всего, нужно сказать, что это формальное отношение – в том смысле, что оно относится к логическим формам посылок и заключения. Логики выявили, что существуют такие комбинации логических форм посылок и заключения, когда при логической истинности посылок невозможно, чтобы заключение оказалось ложным. Это и было названо отношением логического следования

Важно помнить, что в данном случае речь идёт именно о логической, а не фактической истинности высказываний. Мы уже сталкивались с логическим следованием на примере правильных модусов силлогизмов. Модус первой фигуры Barbara является правильным вне зависимости от того, что именно мы подставим на место субъекта, предиката и среднего термина, то есть в нём посылки и заключение связаны отношением логического следования

Другое дело, если мы берём ложные посылки, то, конечно, и заключение будет ложным, но сам модус в этом не виноват: при фактической истинности посылок он всегда гарантирует истинность заключения, просто благодаря определённой комбинации входящих в него логических форм высказываний

Модус первой фигуры Barbara является правильным вне зависимости от того, что именно мы подставим на место субъекта, предиката и среднего термина, то есть в нём посылки и заключение связаны отношением логического следования. Другое дело, если мы берём ложные посылки, то, конечно, и заключение будет ложным, но сам модус в этом не виноват: при фактической истинности посылок он всегда гарантирует истинность заключения, просто благодаря определённой комбинации входящих в него логических форм высказываний.

Далее, дедуктивные рассуждения в свою очередь могут быть прямыми и непрямыми. Опять же все рассмотренные нами умозаключения представляли собой примеры прямого способа построения дедукции. Прямые дедуктивные построения строятся таким образом, что мы непосредственно переходим от посылок к заключению. Практически все разновидности простых базовых умозаключений являются прямыми. Однако в более сложных случаях непосредственный переход от посылок к заключению не всегда возможен, поэтому приходится прибегать к различным приёмам, которые косвенным образом всё же позволяют обосновать тезис с помощью имеющихся аргументов.

Классификация простых суждений

По качеству

• Утвердительные — S есть P. Пример: «Люди пристрастны к самим себе».
• Отрицательные — S не есть P. Пример: «Люди не поддаются лести».

По объёму

• Общие — суждения, которые справедливы относительно всего объёма понятия (Все S суть P). Пример: «Все растения живут».
• Частные — суждения, которые справедливы относительно части объёма понятия (Некоторые S суть P). Пример: «Некоторые растения хвойные».
• Единичные

По отношению

• Категорические — суждения, в которых сказуемое утверждается относительно субъекта без ограничений во времени, в пространстве или обстоятельствах; безусловное суждение (S есть P). Пример: «Все люди смертны».
• Условные — суждения, в которых сказуемое ограничивает отношение каким-либо условием (Если А есть В, то С есть D). Пример: «Если дождь пойдет, то почва будет мокрая». Для условных сужденийОснование — это (предыдущее) суждение, которое содержит условие.
• Следствие — это (последующее) суждение, которое описывает ситуацию, образующуюся при выполнении условия.

По отношению между подлежащим и сказуемым

Логический квадрат, описывающий отношения между категорическими суждениями

Субъект и предикат суждения могут быть распределены

(индекс «+») илине распределены (индекс «-»).

• Распределено — когда в суждении подлежащее (S) или сказуемое (P) берется в полном объёме.
• Не распределено — когда в суждении подлежащее (S) или сказуемое (P) берется не в полном объёме.

Суждения А (обще-утвердительные суждения)

Распределяет своё подлежащее (S), но не распределяет своё сказуемое (P)

Объём подлежащего (S) меньше объёма сказуемого (Р)

Прим.: «Все рыбы суть позвоночные»

Объёмы подлежащего и сказуемого совпадают

Прим.: «Все квадраты суть параллелограммы с равными сторонами и равными углами»

Суждения Е (обще-отрицательные суждения)

Распределяет как подлежащее (S), так и сказуемое (P)

В этом суждении мы отрицаем всякое совпадение между подлежащим и сказуемым

Прим.: «Ни одно насекомое не есть позвоночное»

Суждения I (частно-утвердительные суждения)

Ни подлежащие (S), ни сказуемые (P) не распределены

Часть класса подлежащего входит в класс сказуемого.

Прим.: «Некоторые книги полезны»

Прим.: «Некоторые животные суть Позвоночные»

Суждения О (частно-отрицательные суждения)

Распределяет своё сказуемое (Р), но не распределяет своё подлежащее (S) В этих суждениях мы обращаем внимание на то, что есть несовпадающего между ними (заштрихованная область)

Прим.: «Некоторые животные не суть позвоночные (S)»

Прим.: «Некоторые змеи не имеют ядовитых зубов (S)»

таблица распределения подлежащего и сказуемого

Подлежащее (S)	Сказуемое (P)
о-у	А	распределено	нераспределено
о-о	Е	распределено	распределено
ч-у	I	нераспределено	нераспределено
ч-о	О	нераспределено	распределено

Общая классификация:

• общеутвердительные (A ) — одновременно общие и утвердительные(«Все S+ суть P-»)
• частноутвердительное (I ) — частное и утвердительное(«Некоторые S- суть P-») Прим: «Некоторые люди имеют чёрный цвет кожи»
• общеотрицательное (E ) — общее и отрицательные(«Ни один S+ не суть P+») Прим: «Ни один человек не всеведущ»
• частноотрицательное (O ) — частное и отрицательное(«Некоторые S- не суть P+») Прим: «Некоторые люди не имеют чёрного цвета кожи»

Другие

Разделительные —

1) S есть или А, или В, или С

2) или А, или В, или С есть Р когда в суждении остается место неопределенности

Условно-разделительные суждения —

Если А есть В, то С есть D или Е есть F

если есть А, то есть а, или b, или с Прим: « Если кто желает получить высшее образование, то он должен учиться или в университете, или в институте, или в академии»

• Суждения тождества — понятия субъекта и предиката имеют один и тот же объём. Пример: «Всякий равносторонний треугольник есть равноугольный треугольник».
• Суждения подчинения — понятие с менее широким объёмом подчиняется понятию с более широким объёмом. Пример: «Собака есть домашнее животное».
• Суждения отношения — именно пространства, времени, отношения. Пример: «Дом находится на улице».

• Экзистенциальные суждения или суждения существования — это такие суждения, которые приписывают только лишь существование.
• Аналитические суждения — суждения, в которых мы относительно субъекта высказываем нечто такое, что в нём уже содержится.
• Синтетические суждения — суждения, расширяющие познание. В них не раскрывается содержание подлежащего, а присоединяется нечто новое.

Обращение

В ходе операции обращения субъект и предикат суждения меняются местами (обращаются), при этом не меняется качество суждения.

Виды обращения (от распределенности терминов исходного суждения):

1) чистое обращение;

Если термины суждения оба распределены или оба не распределены, то обращение является чистым (простым). При таком обращении не меняется количественная характеристика суждения.

Например:

«Некоторые студенты проживают в общежитии».

Для преобразования данного суждения посредством операции обращения необходимо изобразить с помощью круговых диаграмм Эйлера отношение между субъектом «студенты» и предикатом «проживающие в общежитии». Эти понятия частично совпадают, оба термина не распределены, поэтому обращение будет чистым.Преобразованное суждение:

«Некоторые проживающие в общежитии студенты».

2) обращение с ограничением.

В случае, когда распределенность терминов суждения разная, обращение будет с ограничением, при котором поменяется количественная характеристика суждения.

Например:

«Граждане России имеют право на образование».

Отношение между понятием субъекта «граждане России» и понятием предиката «имеющие право на образование» является отношением подчинения, где предикат — подчиняющее понятие, а субъект — подчиненное.

Термин субъекта распределен, а предиката не распределен, поэтому обращение будет с ограничением и поменяется количественная характеристика суждения.

Преобразованное суждение:

«Некоторые имеющие право на образование — граждане России».

Правила обращения различных типов суждений:

1. Суждения типа А в основном обращаются с ограничением. Исключением являются общеутвердительные суждения, в которых объемы понятий субъекта и предиката совпадают (выделяющие суждения и определения), поэтому оба термина являются распределенными, а обращение будет чистым.
2. Суждения типа J в основном преобразуются посредством чистого обращения, поскольку в этом типе суждений понятия субъекта и предиката частично совпадают. Исключением являются частноутвердительные выделяющие суждения, в которых объем предиката полностью входит в объем субъекта. Предикат распределен, а субъект не распределен. Преобразование этих суждений будет обращением с ограничением.
3. Суждения типа Е всегда обращаются без ограничения. Оба термина суждения всегда распределены, поскольку в таких суждениях весь объем субъекта исключается из всего объема предиката. Обращение будет чистым.
4. Суждения типа О не обращаются, к ним эта операция неприменима.

Точно так же, как и при выполнении операции превращения, в обращении необходимо увидеть, где оно — новое знание.

Если, как мы знаем, субъект — это то, о чем говорится в суждении, а предикат — то, что говорится о субъекте, и большую смысловую нагрузку несет именно предикат, то в результате выполнения операции обращения мы в новом суждении существенно уточняем наше представление об обоих терминах суждения.

Пример

Вспомните суждение «Мы не рабы». Какое суждение получится в результате обращения «Рабы не мы»? Если в первом суждении говорится о нас и о том, что никто из нас не является рабом, то во втором преобразованном суждении уже говорится о рабах и о том, что никто из рабов не является нами.

Связь мышления с умозаключениями

Как уже говорилось ранее, мышление непосредственно связано с умозаключениями. Это происходит по той причине, что последние являются основным элементом мыслительного процесса. При этом надо учитывать, что умозаключения включают в себя несколько составляющих. Это суждения и выводы. Умозаключения принципиально отличаются от последних, так как являются необходимой составляющей любой фразы, принадлежащей к этому типу. Вывод является частью умозаключения, но последнее не является выводом

Это важно понимать

Умозаключения — это базовая категория мышления, на которой человек строит свои логические цепочки. Любая наука, даже та, которая считается высосанной из пальца, все равно должна базироваться на чистой логике. Понятие умозаключения достаточно простое, чтобы его можно было активно использовать при построении разных речей.

При этом важно понимать, что не каждое является правильным. Поэтому нужно уметь определять истинность каждого готового заключения

А вот это является достаточно тяжелой задачей. Каждое логическое умозаключение должно базироваться на определенных критериях истинности, которые мы сейчас и разберем. Именно на них должно базироваться правильное мышление.

Что такое рассуждение?

Рассуждение появляется тогда, когда делается цепочка из большого количества умозаключений. Каждое из них может стать предпосылкой для дальнейшей логической цепочки. Вся наша жизнь состоит из рассуждений. Даже если человек пересказывает события, которые произошли в его жизни, все равно это можно считать рассуждениями. Ведь он пересказывает связанные между собой факты, которые по сути являются теми же самыми утверждениями, пусть и находящимися в совершенно других грамматических категориях. Соответственно, рассуждение является основой для любого монолога. Если же подбирать грамотные речевые обороты, то это может закончиться невероятным успехом

При этом важно понимать, какие умозаключения являются истинными, а какие — ложными. Вот мы плавно подошли к очень интересной теме — «Формы умозаключения»

Их всего две.

Суждение

Суждение как форма мышления предполагает подтверждение или отрицание какого-то факта, события, свойства, особенности, связи. Проявляется оно во фразах, но нужно помнить, что не каждая фраза является суждением. Так, междометие или односложное предложение не относится к этой форме мышления (примеры: «Ой!», «Как же так?»).

Предложения, как правило, имеют повествовательный характер: «Земля вращается вокруг Солнца».

Суждение может быть истинным или ложным, что определяется логикой. Первое предполагает наличие одного субъекта с характеристиками или сравнение двух субъектов.

При разделении простого суждения слова перестают нести смысловую нагрузку. Пример: «Мышь меньше кошки». Если это предложение разделить на два, смысл теряется.

Суждения сложные представляют собой различные комбинации, которые состоят из сложного и простого, двух сложных или двух простых суждений. Примеры: «Если пройдет град, растения могут пострадать». Здесь «растения могут пострадать» выступает в качестве простого суждения.

Суждение как форма мышления сложного характера невозможно без грамматических связок («но», «или», «и», «если так, то…», «когда…, то…» и т. д.).

Необходимо различать суждение и другие логические формы мышления: понятие выражается словом, а умозаключение выводом.

https://youtube.com/watch?v=N2a9hxvA4YU

Эта форма мышления также может быть:

• утвердительной («Ботаника – наука о растениях», «Тигр является хищником»);
• отрицательной («Это предложение построено неправильно», «В российских городах не гуляют медведи на улицах»).

Существует и другая классификация. Общее суждение предполагает утверждение (отрицание), которое относится к явлениям, субъектам, объединенных с помощью общего понятия («Все здоровые кошки имеют четыре лапы»). Частное подразумевает часть предметов, субъектов, явлений, которые объединены понятием («Какие-то поэты являются графоманами»). В единичном суждении выражено индивидуальное свойство («Ф.М. Достоевский – автор «Преступления и наказания»»).

По сути суждение открывает содержание понятия (или нескольких) – поэтому для высказывания необходимо знать содержание всех используемых понятий.

Умозаключение

Умозаключения как форма мышления образуется при помощи нескольких суждений. Таким образом, имеющаяся информация дает возможность получать новые знания.

Эта форма мышления относится к высшим, так как соединяет в себе понятия и суждения.

Умозаключение может быть правильным или неправильным. Когда говорят об этом свойстве, то имеют в виду теоретическую возможность проверки, так как правильность вывода – это субъективное явление, которое может проверяться в течение продолжительного времени посредством экспериментов и логических рассуждений.

Между суждением и умозаключением существует тесная связь, так как без первого невозможно второе. Умозаключения бывают:

• дедуктивными, являющимися результатом процесса мыслерассуждения от общего к частному;
• индуктивными – обобщение происходит от частного к общему;
• построенными на аналогии, которая использует свойство явлений и объектов, имеющих схожие признаки.

Взаимодействующие между собой понятие, суждение и умозаключение формируют картину человеческого сознания, восприятия и являются основой для развития интеллекта.

Яркий пример умозаключения – это доказательство геометрических теорем.

Итак, основные формы мышления – три составляющие, без которых невозможен мыслительный процесс. Именно благодаря им мозг человека способен анализировать и синтезировать, выстраивать логические связи, что в результате приводит к интеллектуальному развитию. Изучение этих особенностей мышления относится к основным разделам логики, а также к некоторым отделам психологии. 

Оцените эту статью:

• 4.37

Всего голосов: 317

А все-таки из одной предпосылки может быть умозаключение

Помните, в начале статьи говорилось о том, что невозможно из одной предпосылки формировать умозаключение. Так можете этому частично не верить. Почему? Да потому что есть непосредственные умозаключения. Они и являются таковыми, что вывод делается из одного утверждения. Но при этом, как правило, второе уже непосредственно скрыто в первом утверждении. Они получаются некими гибридами.

Взять, например, выражение: «Все адвокаты — юристы». Из него можно построить вывод «Некоторые юристы — адвокаты». И это будет правильно, несмотря на то что вывод делается из одного утверждения. Тем не менее его можно разложить на несколько. Тогда получится такое умозаключение: «Все адвокаты являются юристами. Поскольку юристы могут работать и в других сферах, то, следовательно, некоторые юристы являются адвокатами». Получается в таком случае умозаключение, сделанное из двух утверждений.

Вообще важно понимать, что любая предпосылка имеет определенную степень общности. Соответственно, их можно разложить на несколько частей, если иметь достаточный уровень знаний и развития способности к логическому анализу синтаксического строения фраз

Так что можно сказать так: непосредственные умозаключения — это вид фраз, вывод которых делается из двух предпосылок, одна из которых опускается по причине очевидности. Как видим, любая предпосылка также может называться таким словом, как «умозаключение». Примеры этого уже приводились ранее. Все достаточно просто, несмотря на то что данная тема кажется такой сложной, не так ли?

Умозаключение: критерии истинности

В философии имеется большое количество критериев истинности, которые следует выучить, чтобы определять, насколько правильное то или иное утверждение. Естественно, это не все показатели, способные измерить истинность, но данные здесь являются основными. Кроме всего прочего, данные критерии не являются стопроцентно верифицированными. Но обо всем по порядку.

1. Соответствие законам логики. То есть, чтобы сказанная фраза была правильной, нужно, чтобы она была логической. О законах логики будет идти речь очень длинная, поэтому было принято решение обобщить.
2. Соответствие ранее открытым законам. Далеко не факт, что закон правильный. Ведь используется при его открытии индуктивный метод. Тем не менее если закон уже открыт, то к нему больше доверия, чем если информация непонятно откуда взялась или вообще противоречит без доказательств данным законам.
3. Соответствие фундаментальным законам. Что здесь имеется в виду? Фундаментальный закон — это тот, который считается основополагающим. То есть фундаментальный закон является неоспоримой истиной. Например, в философии таковой можно считать то выражение, с которого начиналась данная статья: «Я мыслю, а значит, существую». Хотя бывают и другие фундаментальные законы.
4. Экономичность. Выражение должно соответствовать данным параметрам, но при этом не занимать много места. С определенным умозаключением человек должен ознакомиться быстро, независимо от его сложности.
5. Парадоксальность. Данный критерий должен верифицироваться (проверяться), но при этом не быть банальным. Вот, например, в свое время умозаключение «Земля круглая» было парадоксальным. Но как показала практика, оно является истинным. То же самое касается любых других утверждений.
6. Практика. Зачем нам нужно умозаключение, которое невозможно применить на практике? Это попросту нелепо, разве не так?

У нас получилось шесть эффективных критериев истинности любого умозаключения

При этом важно учесть еще один так называемый полукритерий. Если какое-то утверждение произносится малоизвестным человеком, люди с меньшей вероятностью сочтут его истинным

Если же оно говорится авторитетом, то вероятность значительно больше. Соответственно, чем более человек авторитетен, тем более истинным кажется утверждение. Данный фактор важно учитывать.