О корреляциях и корреляционном анализе в дипломных по психологии простыми словами

Свойства и предостережения

Коэффициент корреляции Пирсона является мощным инструментом, но его также нужно использовать с осторожностью. Существуют следующие предостережения в его применении:

Коэффициент Пирсона показывает наличие или отсутствие линейной зависимости. Корреляционно-регрессионный анализ на этом не заканчивается, может оказаться, что переменные все-таки связаны между собой.
Нужно быть осторожным в интерпретировании значения коэффициента. Можно найти корреляцию между размером ноги и уровнем IQ. Но это не означает, что один показатель определяет другой.
Коэффициент Пирсона не говорит ничего о причинно-следственной связи между показателями.

Определение экспериментального исследования

Данное изучение направлено на выявление связи между причиной и следствием. Здесь происходит манипуляция переменной, которая проявляется испытуемым, после наблюдается эффект манипуляции на другую переменную, с которой на самом деле не производится никаких манипуляций. Манипулируемая переменная называется независимой. Ее и проверяют экспериментально, так как она может быть причиной изменений другой, зависимой переменной.

После того, как произошло воздействие независимой переменной, исследователь определенным способом собирает сведения о реакции поведения, о вербальной реакции. Это делается для того, чтоб определить влияния переменной. Если это так, то на основе эксперимента заключается вывод, что независимая переменная является причиной изменений зависимой.

Для примера рассмотрим исследование Семеновой З.Ф. Оно было проведено на студии телевидения и выявляло роли социального статуса коммуникатора (независимая переменная) на восприятие информации реципиента (зависимая переменная).

Эксперимент проводился естественным путем. Т.е. на экскурсию в телестудию пригласили людей и под удобным предлогом предложили посмотреть новости. Люди думали, что они смотрят передачу для эфира. Во всех новостях был представлен один и тот же человек, с одним и тем же сообщением, в одно и том же гриме, но в разных амплуа:

конструктор завод;
бригадир;
ученый;
журналист.

Выборка испытуемых – 667 человек:

мужчин – 291;
женщин – 376.

В каждой группе 20-30 человек. Деятельность людей разная:

рабочие;
инженерно-технические сотрудники;
интеллигенция.

После просмотра новостей всем объясняли цели экскурсии и раздали анкеты для заполнения.

Изначально предполагалось, что социальный статус коммуникатора будет оказывать влияние на отношение испытуемых к сообщению, что и произошло на самом деле. Влияние произошло из-за близости социальной категории, например, рабочим была важна новость от «бригадира». Корреляция иногда была равна +0,88.

Плюс экспериментального исследования:

хороший контроль над переменными.

Природа корреляционного исследования

Существует два вида исследования:

корреляция;
эксперимент.

Рассмотрим каждый из них.

Корреляционное исследование используется в случае, если необходимо дать оценку взаимоотношениям между двумя и более переменными. Т.е. этот метод изучения выявляет связь между данными.

Если одна переменная меняет величину, то со второй происходят следующие изменения. Во-первых, стоит отметить, что это исследование дает сведения о направлении и силе взаимосвязи между двумя данными. Это направление говорит о том, как связаны переменные: позитивно или негативно. Сила взаимосвязи может быть в виде степени точности, также может предсказать величину одной из переменных. Эти два аспекта (сила и направление) являются статистическими критериями, или коэффициентами корреляции (r), который ранжируется от +1,00 до -1,00. Например: переменная А высока, В высока, то корреляция позитивная. Если А высока, а В низка, то корреляция негативная. Если В не связана с А, то корреляция отсутствует.

Социально-психологические исследования не содержит полную корреляцию. Коэффициент редко превышает +0,60:

корреляции от +0,50 до +0,60 являются сильными;
корреляции от +0,30 до +0,50 – умерено сильные;
корреляции ниже от +0,30 или +0,20 – слабые.

Корреляция выше +0,60 бывает в том случае, если ряд факторов, определяющие поведение, мнение и оценки людей.

Используя математическую обработку данных, исследователь может применять разные подходы к вычислению коэффициенты корреляции.

Задачи, виды и показатели корреляционно-регрессионного анализа

Задачи КРА заключаются в:

идентификации наиболее значимых факторов влияния на конкретный показатель деятельности предприятия;
количественном измерении тесноты выявленных связей между показателями;
определении неизвестных причин возникновения связей;
всесторонней оценке факторов, которые признаны наиболее важными для рассматриваемого показателя;
выведении формулы уравнения регрессии;
составлении прогноза возможного результата деятельности при изменении ключевых связанных факторов с учетом возможного влияния других факторных признаков.

КРА подразумевает использование нескольких видов корреляционных и регрессионных методов. Зависимости выявляются при помощи корреляций таких типов:

парная, если связь устанавливается с участием двух признаков;
частная – взаимосвязь оценивается между искомым показателем и одним из ключевых факторов, при этом условием задается постоянное значение комплекса других факторов (то есть числовое выражение всех остальных факторов в любых ситуациях будет приниматься за определенную неизменную величину);
множественная – основу исследования составляет влияние на показатель деятельности не одного фактора, а сразу нескольких критериев (двух и более).

СПРАВОЧНО! Выявленные показатели степени тесноты связей отражаются коэффициентом корреляции.

На выбор коэффициента влияет шкала измерения признаков:

Шкала номинальная, которая предназначена для приведения описательных характеристик объектов.
Шкала ординальная нужна для вычисления степени упорядоченности объектов в привязке к одному и более признакам.
Шкала количественная используется для отражения количественных значений показателей.

Регрессионный анализ пользуется методом наименьших квадратов. Регрессия может быть линейной и множественной. Линейный тип предполагает модель из связей между двумя параметрами. Например, при наличии таких двух критериев, как урожайность клубники и полив, понятно, что именно объем поступающей влаги будет влиять на объем выращенной и собранной клубники. Если полив будет чрезмерным, то урожай пропадет. Урожайность же клубники никак не может воздействовать на систему полива.

Множественная регрессия учитывает более двух факторов одновременно. В случае с клубникой при оценке ее урожайности могут использоваться факторы полива, плодородности почвы, температурного режима, отсутствия слизняков, сортовые особенности, своевременность внесения удобрений. Все перечисленные показатели в совокупности оказывают комплексное воздействие на искомое значение – урожайность ягод.

Система показателей анализа формируется критериями классификации. Например, при экстенсивном типе развития бизнеса в качестве показателей могут выступать такие факторы:

количество сотрудников;
число заключенных договоров за отчетный период;
посевные площади;
прирост поголовья скота;
расширение дилерской сети;
объем основных фондов.

При интенсивном типе развития могут применяться следующие показатели:

производительность труда;
рентабельность;
урожайность;
фондоотдача;
ликвидность;
средний объем поставок в отчетном периоде по одному договору.

Проведение процедуры корреляционного анализа

Как ты уже поняла, корреляционный анализ позволяет проверить выдвинутую ученым гипотезу и собрать доказательную базу путем использования математических и статистических приемов. Это позволяет установить причину и следствие конкретных психологических событий явлений.

Если коэффициент корреляции вышел со знаком «-», то это свидетельствует об отсутствии явной зависимости между изучаемыми явлениями. Положительное значение будет свидетельствовать об обратном. Также в некоторых методиках возможно значение корреляции будет зависеть в зависимости от его значения и принадлежности к критической области.

Самыми признанными методиками корреляционного анализа, используемыми в психологической науке, являются: коэффициент Пирсона, коэффициент Кендалла и критерий Спирмена. Каждый из методов обладает собственной оригинальностью и условиями применения.

Почему корреляция не синоним причинности?

Последовательность действий при реализации корреляционного анализа следующая:

Сбор необходимых материалов посредством проведения наблюдения, эксперимента, анкетирования, тестов;
Перевод информации в числовой вид с учетом необходимых обозначений. Для этого используется ранжирование. Ранжирование — это приписывание объектам чисел в зависимости от степени выраженности измеряемого свойства;
Построение специальной таблицы для анализа данных и расчета показателей;
Сопоставление полученных результатов с утвержденными стандартами (нормой);
Формулировка выводов исследования.

Корреляция в психологическом исследовании

Корреляционный метод в психологии дает исследователям возможность получить максимум полезной информации из экспериментальных данных, выявить взаимосвязи между ними и степень влияния факторов друг на друга.

Корреляция в психологических исследованиях может выявить зависимость между показателями:

прямую (положительную);
обратную (отрицательную).

Корреляция между показателями выражается цифрами в диапазоне от 1 до -1. Коэффициенты корреляции, имеющие статистическую ценность, выводятся путем сравнения полученного в ходе эксперимента показателя с критическим значением. Его определяют по объему выборки. Чем она больше, тем меньше показатель критического значения.

Проблемы применения

В основе корреляционно-регрессионного анализа лежат следующие предположения:

Наблюдения считаются независимыми (пятикратное выпадение «орла» никак не влияет на результат следующего подбрасывания монетки).
В корреляционном анализе обе переменные рассматриваются как случайные. В регрессионном – только одна (зависимая).
При проверке гипотезы должно соблюдаться нормальное распределение. Изменение зависимой переменной должно быть одинаковым для каждой величины на оси абсцисс.
Корреляционная диаграмма – это только первая проверка гипотезы о взаимоотношениях между двумя рядами параметров, а не конечный результат анализа.

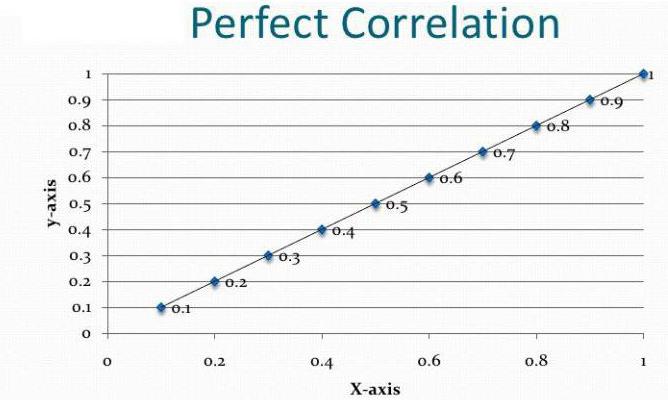
Назначение корреляционного анализа

Корреляционный анализ позволяет найти зависимость одного показателя от другого, и в случае ее обнаружения – вычислить коэффициент корреляции (степень взаимосвязи), который может принимать значения от -1 до +1:

если коэффициент отрицательный – зависимость обратная, т.е. увеличение одной величины приводит к уменьшению второй и наоборот.
если коэффициент положительный – зависимость прямая, т.е. увеличение одного показателя приводит к увеличению второго и наоборот.

Сила зависимости определяется по модулю коэффициента корреляции. Чем больше значение, тем сильнее изменение одной величины влияет на другую. Исходя из этого, при нулевом коэффициенте можно утверждать, что взаимосвязь отсутствует.

Что такое корреляционно-регрессионный анализ (КРА) предприятия?

Корреляционно-регрессионный анализ (КРА) на предприятиях используется для выявления связей между несколькими факторами хозяйственной деятельности и оценки степени взаимозависимости выбранных для анализа критериев. Методика использует два алгоритма действий:

Корреляция, которая направлена на построение моделей связей.
Регрессия, используемая для прогнозирования событий на основе наиболее подходящей для ситуации модели связей.

Анализ проводится в несколько шагов:

постановка задач проведения исследования;
массовый сбор информации: систематизация статистических данных по конкретным показателям деятельности предприятия в динамике за несколько периодов;
этап создания модели связей;
анализ функционирования модели, оценка ее эффективности.

Для проведения КРА необходимо использовать показатели в едином измерителе, все они должны иметь числовое значение.

ОБРАТИТЕ ВНИМАНИЕ! Для достоверности данных и работоспособности модели сведения должны быть собраны за длительный отрезок времени. Для полноты анализа надо устранить количественные ограничения на показатели модели, должно соблюдаться условие постоянной временной и территориальной структуры рассматриваемой совокупности элементов

Для полноты анализа надо устранить количественные ограничения на показатели модели, должно соблюдаться условие постоянной временной и территориальной структуры рассматриваемой совокупности элементов.

Какие существуют особенности анализа показателей финансово-хозяйственной деятельности экономического субъекта в рамках обязательного аудита?

Линейная и множественная регрессия

Предположим, что X и Y – это две связанные переменные. Регрессионный анализ позволяет предсказать величину одной из них на основе значений другой. Например, зрелость и возраст – это зависимые признаки. Зависимость между ними отражается с помощью линейной регрессии. Фактически можно выразить X через Y или наоборот. Но зачастую только одна из линий регрессии оказывается правильной. Успех анализа во многом зависит от правильности определения независимой переменной. Например, у нас есть два показателя: урожайность и объем выпавших осадков. Из житейского опыта становится ясно, что первое зависит от второго, а не наоборот.

Множественная регрессия позволяет рассчитать неизвестную величину на основе значений трех и более переменных. Например, урожайность риса на акр земли зависит от качества зерна, плодородности почвы, удобрений, температуры, количества осадков. Все эти параметры влияют на совокупный результат. Для упрощения модели используются следующие допущения:

Зависимость между независимой и влияющими на нее характеристиками является линейной.
Мультиколлинеарность исключена. Это означает, что зависимые переменные не связаны между собой.
Гомоскедастичность и нормальность рядов чисел.

Как рассчитать коэффициент корреляции

Коэффициенты Пирсона и Спирмена можно рассчитать вручную. Это может понадобиться при углубленном изучении статистических методов.

Однако в большинстве случаев при решении прикладных задач, в том числе и в психологии, можно проводить расчеты с помощью специальных программ.

Расчет с помощью электронных таблиц Microsoft Excel

Вернемся опять к примеру со студентами и рассмотрим данные об уровне их интеллекта и длине прыжка с места. Занесем эти данные (два столбца) в таблицу Excel.

Переместив курсор в пустую ячейку, нажмем опцию «Вставить функцию» и выберем «КОРРЕЛ» из раздела «Статистические».

Формат этой функции предполагает выделение двух массивов данных: КОРРЕЛ (массив 1; массив»). Выделяем соответственно столбик с IQ и длиной прыжков.

Далее нажимаем галочку (то есть, рассчитать) и получаем значение , в нашем случае 0,038. Как видим, коэффициент не равен нулю, хотя и очень близок к нему.

В таблицах Excel реализована формула расчета только коэффициента Пирсона.

Расчет с помощью программы STATISTICA

Заносим данные по интеллекту и длине прыжка в поле исходных данных. Далее выбираем опцию «Непараметрические критерии», «Спирмена». Выделяем параметры для расчета и получаем следующий результат.

Как видно, расчет дал результат 0,024, что отличается от результата по Пирсону – 0,038, полученной выше с помощью Excel. Однако различия незначительны.

Корреляция и диверсификация

Как знания о корреляции активов могут помочь лучше вкладывать деньги? Думаю, вы все хорошо знакомы с золотым правилом инвестора — не клади все яйца в одну корзину. Речь, естественно, идёт о диверсификации, которая неразрывно связана с понятием корреляции. Это улавливается даже из названия — английское diversify означает «разнообразить», а как коэффициент корреляции как раз показывает схожесть или различие двух явлений.

Другими словами, инвестировать в финансовые инструменты с высокой корреляцией не очень хорошо. Почему? Все просто — похожие активы плохо диверсифицируются. Вот пример портфеля двух активов с корреляцией +1:

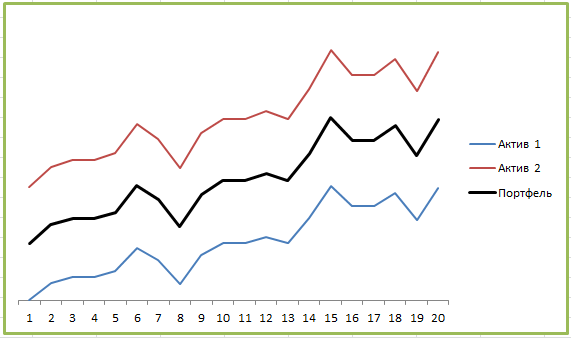
Как видите, график портфеля во всех деталях повторяет графики каждого из активов — рост и падение обоих активов синхронны. Диверсификация в теории должна снижать инвестиционные риски за счёт того, что убытки одного актива перекрываются за счёт прибыли другого, но здесь этого не происходит совершенно. Все показатели просто усредняются:

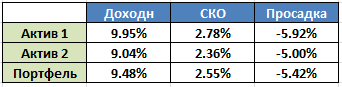
Портфель даёт небольшой выигрыш в снижении рисков — но только по сравнению с более доходным Активом 1. А так, никаких преимуществ по сути нет, нам лучше просто вложить все деньги в Актив 1 и не париться.

А вот пример портфеля двух активов с корреляцией близкой к 0:

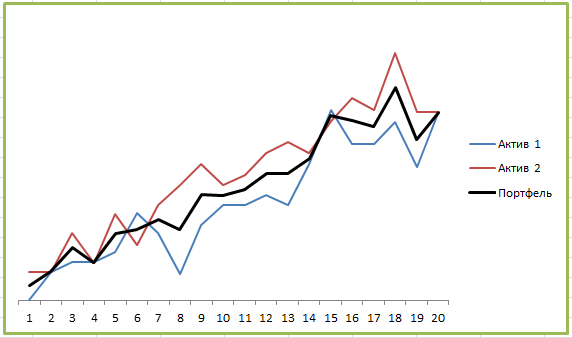
Где-то графики следуют друг за другом, где-то в противоположных направлениях, какой-либо однозначной связи не наблюдается. И вот здесь диверсификация уже работает:

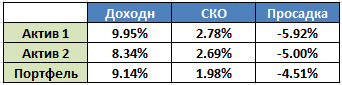
Мы видим заметное снижение СКО, а значит портфель будет менее волатильным и более стабильно расти. Также видим небольшое снижение максимальной просадки, особенно если сравнивать с Активом 1. Инвестиционные инструменты без корреляции достаточно часто встречаются и из них имеет смысл составлять портфель.

Впрочем, это не предел. Наиболее эффективный инвестиционный портфель можно получить, используя активы с корреляцией -1:

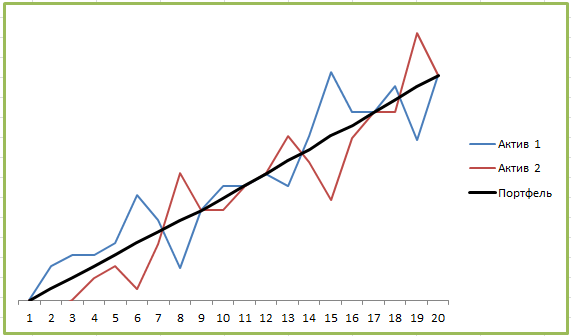
Уже знакомое вам «зеркало» позволяет довести показатели риска портфеля до минимальных:

Несмотря на то, что каждый из активов обладает определенным риском, портфель получился фактически безрисковым. Какая-то магия, не правда ли? Очень жаль, но на практике такого не бывает, иначе инвестирование было бы слишком лёгким занятием.

Зачем использовать регрессионный анализ?

Корреляционная зависимость предполагает нахождение отношений между величинами. Причинно-следственная связь в этом случае остается за кадром. Задачи корреляционного и регрессионного анализа совпадают только в плане подтверждения наличия зависимости между значениями двух величин. Однако первоначально исследователь не обращает внимания на возможность причинно-следственной связи. В регрессионном анализе всегда есть две переменные, одна и которых является зависимой. Он проходит в несколько этапов:

Выбор правильной модели с помощью метода наименьших квадратов.
Выведение уравнения, описывающего влияние изменения независимой переменной на другую.

Например, если мы изучаем влияние возраста на рост человека, то регрессионный анализ может помочь предсказать изменения с течением лет.

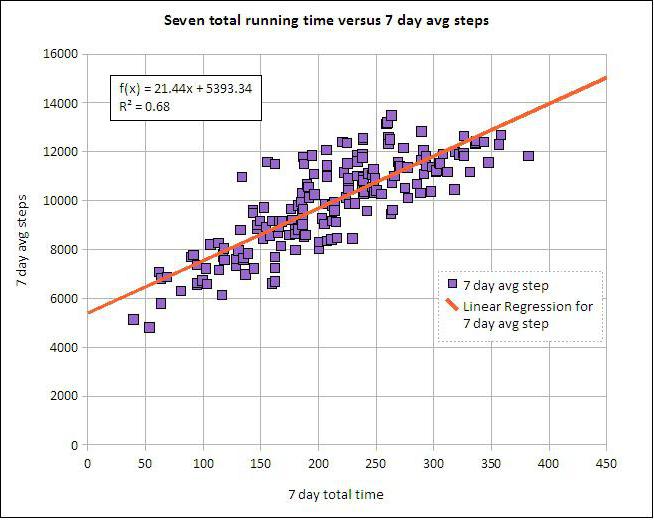
Корреляционно-регрессионный анализ: пример

Предположим, происходит оценка эффективности деятельности десяти предприятий. У нас есть двое судей, которые выставляют им баллы. Корреляционно-регрессионный анализ предприятия в этом случае не может быть проведен на основе линейного коэффициента Пирсона. Нас не интересует взаимосвязь между оценками судей. Важны ранги предприятий по оценке судей.

Данный тип анализа имеет следующие преимущества:

Непараметрическая форма отношений между исследуемыми величинами.
Простота использования, поскольку ранги могут приписываться как в порядке возрастания значений, так и убывания.

Единственное требование данного типа анализа – это необходимость конвертации исходных данных.

Примеры

Необходимо определить взаимосвязь двух переменных: уровня интеллектуального развития (по данным проведенного тестирования) и количества опозданий за месяц (по данным записей в учебном журнале) у школьников.

Исходные данные представлены в таблице:

№	Данные по уровню IQ (x)	Данные по количеству опозданий (y)
1	100	6
2	115	2
3	117	1
4	119	1
5	134	2
6	94	8
7	105	3
8	103	4
9	111	3
10	124
Сумма	1122	30
Среднее арифметическое	112,2	3

Чтобы дать правильную интерпретацию полученному показателю, необходимо проанализировать знак коэффициента корреляции (+ или -) и его абсолютное значение (по модулю).

В соответствии с таблицей классификации коэффициента корреляции по силе делаем вывод о том, rxy = -0,827 – это сильная отрицательная корреляционная зависимость. Таким образом, количество опозданий школьников имеет очень сильную зависимость от их уровня интеллектуального развития. Можно сказать, что ученики с высоким уровнем IQ опаздывают реже на занятия, чем ученики с низким IQ.

Важно! Принято считать, что чем r ближе по модулю к 1, тем ближе связь между анализируемыми переменными к линейной. Если величина r близка к -1, то связь обратная (c возрастанием переменной х переменная у убывает).. Коэффициент корреляции может применяться как учеными для подтверждения или опровержения предположения о зависимости двух величин или явлений и измерения ее силы, значимости, так и студентами для проведения эмпирических и статистических исследований по различным предметам

Необходимо помнить, что этот показатель не является идеальным инструментом, он рассчитывается лишь для измерения силы линейной зависимости и будет всегда вероятностной величиной, которая имеет определенную погрешность

Коэффициент корреляции может применяться как учеными для подтверждения или опровержения предположения о зависимости двух величин или явлений и измерения ее силы, значимости, так и студентами для проведения эмпирических и статистических исследований по различным предметам. Необходимо помнить, что этот показатель не является идеальным инструментом, он рассчитывается лишь для измерения силы линейной зависимости и будет всегда вероятностной величиной, которая имеет определенную погрешность.

Корреляционный анализ применяется в следующих областях:

экономическая наука;
астрофизика;
социальные науки (социология, психология, педагогика);
агрохимия;
металловедение;
промышленность (для контроля качества);
гидробиология;
биометрия и т.д.

Причины популярности метода корреляционного анализа:

Относительная простота расчета коэффициентов корреляции, для этого не нужно специальное математическое образование.
Позволяет рассчитать взаимосвязи между массовыми случайными величинами, которые являются предметом анализа статистической науки. В связи с этим этот метод получил широкое распространение в области статистических исследований.

Надеюсь, теперь вы сможете отличить функциональную взаимосвязь от корреляционной и будете знать, что когда вы слышите по телевидению или читаете в прессе о корреляции, то под ней подразумевают положительную и достаточно значимую взаимозависимость между двумя явлениями.

Понятие корреляции

Корреляция (от латинского «correlatio» – соотношение, взаимосвязь) – математический термин, который означает меру статистической вероятностной зависимости между случайными величинами (переменными).

Пример: возьмем два вида взаимосвязи:

Первый – ручка в руке человека. В какую сторону движется рука, в такую сторону и ручка. Если рука находится в состоянии покоя, то и ручка не будет писать. Если человек чуть сильнее надавит на нее, то след на бумаге будет насыщеннее. Такой вид взаимосвязи отражает жесткую зависимость и не является корреляционным. Это взаимосвязь – функциональная.
Второй вид – зависимость между уровнем образования человека и прочтением литературы. Заранее неизвестно, кто из людей больше читает: с высшим образованием или без него. Эта связь – случайная или стохастическая, ее изучает статистическая наука, которая занимается исключительно массовыми явлениями. Если статистический расчет позволит доказать корреляционную связь между уровнем образованности и прочтением литературы, то это даст возможность делать какие-либо прогнозы, предсказывать вероятностное наступление событий. В этом примере с большой долей вероятности можно утверждать, что больше читают книги люди с высшим образованием, те, кто более образован. Но поскольку связь между данными параметрами не функциональная, то мы можем и ошибиться. Всегда можно рассчитать вероятность такой ошибки, которая будет однозначно невелика и называется уровнем статистической значимости (p).

Примерами взаимосвязи между природными явлениями являются: цепочка питания в природе, организм человека, который состоит из систем органов, взаимосвязанных между собой и функционирующих как единое целое.

Каждый день мы сталкиваемся с корреляционной зависимостью в повседневной жизни: между погодой и хорошим настроением, правильной формулировкой целей и их достижением, положительным настроем и везением, ощущением счастья и финансовым благополучием. Но мы ищем связи, опираясь не на математические расчеты, а на мифы, интуицию, суеверия, досужие домыслы. Эти явления очень сложно перевести на математический язык, выразить в цифрах, измерить. Другое дело, когда мы анализируем явления, которые можно просчитать, представить в виде цифр. В таком случае мы можем определить корреляцию с помощью коэффициента корреляции (r), отражающего силу, степень, тесноту и направление корреляционной связи между случайными переменными.

Сильная корреляция между случайными величинами – свидетельство наличия некоторой статистической связи конкретно между этими явлениями, но эта связь не может переноситься на эти же явления, но для другой ситуации. Часто исследователи, получив в расчетах значительную корреляцию между двумя переменными, основываясь на простоте корреляционного анализа, делают ложные интуитивные предположения о существовании причинно-следственных взаимосвязей между признаками, забывая о том, что коэффициент корреляции носит вероятностный характер.

Пример: количество травмированных во время гололеда и число ДТП среди автотранспорта. Эти величины будут коррелировать между собой, хотя они абсолютно не взаимосвязаны между собой, а имеют только связь с общей причиной этих случайных событий – гололедицей. Если же анализ не выявил корреляционной взаимосвязи между явлениями, это еще не является свидетельством отсутствия зависимости между ними, которая может быть сложной нелинейной, не выявляющейся с помощью корреляционных расчетов.

Первым, кто ввел в научный оборот понятие корреляции, был французский палеонтолог Жорж Кювье. Он в XVIII веке вывел закон корреляции частей и органов живых организмов, благодаря которому появилась возможность восстанавливать по найденным частям тела (останкам) облик всего ископаемого существа, животного. В статистике термин корреляции впервые применил в 1886 году английский ученый Френсис Гальтон. Но он не смог вывести точную формулу для расчета коэффициента корреляции, но это сделал его студент – известнейший математик и биолог Карл Пирсон.

Специфика ранговой корреляции

Рассмотрим коэффициент ранговой корреляции Спирмена (r), так как именно его часто применяют в социально-психологических исследованиях благодаря своей универсальности и простоте. Универсальность, т.е. применим ко всем данным, проста – легко вычисляется «вручную».

Пример. Для того чтобы понять роль мастера в организации, были собраны данные в виде оценочных суждений от работников разного иерархического уровня. В исследование рассматривали вопрос взаимосвязи восприятия мастера рабочими низкого иерархического уровня и высшего с самооценкой самого мастера. Для оценивания были представлены такие качества, как:

требовательность;
настойчивость;
уравновешенность;
доброта;
скромность;
дисциплинированность;
справедливость;
оптимизм и т.д.

В результате была выявлена положительная корреляция между самооценкой мастера и оценкой рабочих: r = +0,39. Положительная связь наблюдается также между самооценкой мастера и вышестоящих коллег:r = +0,33, но в данном случае носит менее устойчивую связь. Самый низкий коэффициент был выявлен между оценками мастера руководством цеха и рабочими r = +0,18.

Вывод

Рассматриваемая ситуация не всегда имеет одинаковую оценку и, поэтому может быть производной от других социальных ролей, которые связаны с принадлежностью этой личности к другой группе, являющейся значимой. Из полученных данных видно, что рабочие играют для мастера референтную роль, а цеховые руководители нет. Конечно, этот результат требует детальной проверки.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Исходя из выше сказанного, было выявлено несколько выводов, которые описывали восприятие и понимание личности и работы мастера в зависимости от социально-демографических и ролевых характерных черт субъектов и объектов оценки.

Плюсы такого исследования: