Теория полей и струн

Заметки

Это зависит от правильного выбора калибр. φ и А не определяются однозначно ρ и J; скорее, они определены только с точностью до некоторой скалярной функции ж(р, т) известный как калибр. Формализм запаздывающего потенциала требует выбора Датчик Лоренца.
Это эквивалентно выбору единиц измерения расстояния и времени в виде световых секунд и секунд или световых лет и лет. Выбор c = 1 позволяет упростить уравнения. Например, E = MC2 сводится к E = м (поскольку c2 = 1, без учета единиц). Это снижает сложность выражений, сохраняя при этом акцент на основных принципах. Эту «хитрость» необходимо учитывать при проведении реальных численных расчетов.

Возможная теория

Термин « теория потенциала » возник из-за того факта, что в физике XIX века фундаментальные силы природы считались производными от скалярных потенциалов, которые удовлетворяли уравнению Лапласа . Пуассон обратился к вопросу об устойчивости планетных орбит , который уже был решен Лагранжем в первой степени приближения на основе сил возмущения, и вывел уравнение Пуассона , названное в его честь. Общий вид этого уравнения:

∇2ϕзнак равноσ{\ displaystyle \ nabla ^ {2} \ phi = \ sigma}

где σ — функция источника (как плотность, величина на единицу объема), а φ — скалярный потенциал, для которого нужно найти.

В ньютоновской гравитации; массы являются источниками поля, так что силовые линии заканчиваются на объектах, обладающих массой. Точно так же заряды являются источниками и стоками электростатических полей: положительные заряды испускают силовые линии электрического поля, а силовые линии заканчиваются отрицательными зарядами. Эти концепции поля также проиллюстрированы в общей теореме о расходимости , в частности в законе Гаусса для гравитации и электричества. Для случаев не зависящей от времени гравитации и электромагнетизма поля являются градиентами соответствующих потенциалов

граммзнак равно-∇ϕграмм,Eзнак равно-∇ϕе{\ Displaystyle \ mathbf {g} = — \ nabla \ phi _ {g} \ ,, \ quad \ mathbf {E} = — \ nabla \ phi _ {e}}

таким образом, подставляя их в закон Гаусса для каждого случая, получаем

∇2ϕзнак равно4πграммρграмм,∇2ϕзнак равно-ρеϵ{\ displaystyle \ nabla ^ {2} \ phi = 4 \ pi G \ rho _ {g} \ ,, \ quad \ nabla ^ {2} \ phi = — {\ rho _ {e} \ over \ epsilon _ { 0}}}

где ρ _g — массовая плотность, а ρ _e — плотность заряда .

Кстати, это сходство возникает из — за сходства между законом тяготения Ньютона и закон Кулона .

В случае отсутствия источника (например, вакуума или парных зарядов) эти потенциалы подчиняются уравнению Лапласа :

∇2ϕзнак равно{\ Displaystyle \ набла ^ {2} \ фи = 0}

Для распределения массы (или заряда) потенциал может быть разложен на серию сферических гармоник , а n- й член в серии может рассматриваться как потенциал, возникающий из 2 n- моментов (см. Мультипольное разложение ). Для многих целей в расчетах нужны только члены монополя, диполя и квадруполя.

Почему человек ведет себя неадекватно или заболевает?

Потребности, граничащие с «оболочкой», осознаются, а центральные не осознаются. У тех потребностей, которые не осознаются, заряд сильнее, они больше беспокоят человека — поэтому он испытывает непонятную тревогу.

С потребностью всегда связан комплекс чувств. Если вы сталкиваетесь с агрессией, обвинением, осуждением в адрес вашей потребности, то в какой-то момент вы предпочтете не чувствовать ее. Потребности перестают осознаваться, чтобы человек смог избежать чувства вины, страха, стыда со стороны окружения. Потребность теряет контакт с сенсомоторной зоной и уходит в центр. Человек получает облегчение, он выдыхает, но потребность остается неудовлетворенной, и от этого система будет в состоянии напряжения. Возбуждение есть, но в связи с чем, человек не осознает. В таком случае существуют два способа реализовать эту потребность.

Диффузная («кривая») реализация. Для нее характерен истеричный смех, плач, крик, происходящий непонятно в связи с чем. Женщина хочет внимания, но не говорит об этом, вместо этого плачет или кричит — в этом случае потребность также удовлетворена, но не напрямую. Тем не менее ей становится легче.
Формирование болезни. Например, вместо того чтобы защищать свои границы от нападок других людей или нарушения личного пространства, человек начинает страдать ожирением, астмой или нейродермитом

Любой симптом является способом реализовать потребность, это способ вступить в контакт с другими людьми по самой важной потребности (которую, подчеркну, личность или отрицает, или не осознает). В этом смысле человек может быть «спокоен», потому что в любом случае потребность будет реализована. Если не прямым способом, то через симптом

А заболев определенным недугом, человек покажет, чего хочет.

Если не прямым способом, то через симптом. А заболев определенным недугом, человек покажет, чего хочет.

Мы всегда сосредоточены на чем-то главном.

Многие потребности актуализированы в одно и то же время, поэтому они стоят в определенной очереди.

Но существует принцип прегнантности — фигурой может в настоящий момент являться только одна потребность, самая возбужденная.

Таким образом, мир обладает целостностью — полем. Люди не самостоятельны, они частицы заряженного поля. Если человек попадает в какое-то окружение, оно обязательно повлияет на него так или иначе, произойдут некие изменения. Человек — открытая энергетически система, которая реагирует на явления внешней среды. По «Теории поля» личность фактически не может самостоятельно делать полноценный выбор в жизни, она очень зависима от среды. Поэтому в любой оригинальности мы видим элементы повторяемости.

Теория и экспериментальные данные

Теория поля Изображение 1

Теория поля Изображение 2

Согласно теории поля, жизнь человека состоит из множества различных пространств. Изображение 1 представляет собой пример общего поля или окружающей среды. Изображение 2 показывает человек, и цель у них есть. Это изображение показывает, что есть силы, толкающие человека к своей цели. Пунктирная линия все нужно пройти, чтобы достичь своей цели, и как нужно пройти через множество различных пространств. Физические лица могут иметь ту же цель, но поле, чтобы получить там могут быть разные. СВОЮ поле может быть скорректирована, чтобы получить больше всего в жизни. Некоторые поля могут быть удалены, а некоторые добавляют, все в зависимости от определенных событий, которые происходят в жизни людей.

Теория поля также включает в себя идею , что каждый человек держит другой опыт для ситуации. Это не означает , что опыт двух людей о событии не будет похож, но что там будет какая — то разница. Это приводит к тому , что никакие два опыта не являются одинаковыми для человека , или, как динамическое поле постоянно меняется. Это говорит о том, что динамическое поле , как поток, течет постоянно, слегка меняется. Другая частью теории поля является идеей , что ни одна части поля человека не может рассматриваться как бессмысленно

Каждая часть общего поля должны рассматриваться как имеющие возможное значение и важность. Это должно быть сделано независимо от того, насколько бессмысленно или не важна часть поля может показаться, что все равно должны быть учтены. Совокупность поля индивида кажется , не имеет никаких границ, поскольку исследования показали , что опыт даже младенец из Второй мировой войны , возможно , повлиять на жизнь в дальнейшем, в связи с изменением поля

Это хороший пример того , насколько широка теория поля может охватывать как пред- сознание человека может быть изменено из — за изменения на места , которые произошли до любого крупного развития.

Совокупность поля индивида кажется , не имеет никаких границ, поскольку исследования показали , что опыт даже младенец из Второй мировой войны , возможно , повлиять на жизнь в дальнейшем, в связи с изменением поля. Это хороший пример того , насколько широка теория поля может охватывать как пред- сознание человека может быть изменено из — за изменения на места , которые произошли до любого крупного развития.

Генерация социальных изменений

В рамках объяснения и изменения социальных явлений Левин провел эксперимент с двумя своими учениками (Lewin, Lippitt and White, 1939) и продемонстрировал различия, которые тип лидерства (автократический, демократический и laissez faire) может генерировать в группе. ).

В рамках теории поля он также предложил исследовательский подход, называемый исследованием действий, который направлен на содействие социальным изменениям, основанным на исследовании соответствующих социальных проблем..

Его интерес к этим социальным проблемам привел его к изучению с помощью этого метода расизма, ксенофобии, агрессии и других..

Потребности и то, как мы их реализуем

Потребности человека определяют его поведение. Человек может говорить и думать о себе что угодно, но он будет автоматически действовать исходя из потребностей. В схеме Курта Левина потребности находятся внутри внешней границы, их можно представить в виде «кружков», наполняющих энергетику человека. Например, потребностью является необходимость обрести любимого человека. Индивид может даже отрицать это, но действовать будет по инерции — путешествовать в поисках новых людей, смотреть фильмы про любовь, «случайно» обсуждать это.

Личность — это сложная система, вся жизнедеятельность которой стремится к равновесию. Когда равновесие нарушается (а оно нарушается постоянно, и это есть норма), внутри возникает напряжение.

Стоит сказать, что потребности не существуют изначально, они появляются в результате контакта с окружением. У человека, живущего в Вологодской деревне в семье фермера и живущего в центре Берлина в окружении рок-музыкантов, потребности будут разные.

Огромный информационный поток, особенно реклама, формирует у человека столько потребностей, что накапливается их переизбыток. Это перегружает психику человека, порождает тревогу непонятного для него генеза. К примеру, если вдуматься, все, что мы покупаем или мечтаем купить, — совершенно не нужно. Например, в гаджетах мы используем не более 25% функций, хотя меняем их раз в полгода ради обновлений.

Приложения [ править ]

Теория поля классов используется для доказательства двойственности Артина-Вердье . Очень явная теория полей классов используется во многих областях алгебраической теории чисел, таких как теория Ивасавы и теория модулей Галуа.

Большинство основных достижений в отношении соответствия Ленглендса для числовых полей, гипотезы BSD для числовых полей и теории Ивасавы для числовых полей используют очень явные, но узкие методы теории полей классов или их обобщения. Поэтому открытый вопрос состоит в том, чтобы использовать обобщения общей теории полей классов в этих трех направлениях.

Основные тезиcы для объяснения Теории психологического поля

Объяснение поведения включает более широкий круг явлений, нежели только раздражители и реакции. Для анализа ситуации рассматривается взаимосвязь субъекта с окружающим его пространством и обществом;
Ситуацию следует интерпретировать так, как она представляется субъекту. К основным компонентам причинно-следственного анализа относятся воспринимаемые (отраженные субъектом) особенности окружения, которые предоставляют человеку различные возможности для действия;
В основе всякого поведения лежат силы, из которых главными являются потребности;
Уравнение поведения:
поведение есть функция личностных факторов и факторов окружения

Гештáльт-психолóгия (от нем. Gestalt — личность, образ, форма) — это общепсихологическое направление, которое связано с попытками объяснения прежде всего восприятия, мышления и личности. В качестве основного объяснительного принципа гештальтпсихология выдвигает принцип целостности. Основана Максом Вертгеймером, Вольфгангом Кёлером и Куртом Коффкой в 1912 году.

Формулировка на современном языке [ править ]

На современном математическом языке теорию поля классов можно сформулировать следующим образом. Рассмотрим максимальное абелево расширение А локального или глобального поля K . Он имеет бесконечную степень над K ; группа Галуа G группы A над K является бесконечной проконечной группой , а значит, компактной топологической группой , и она абелева. Центральные цели теории полей классов: описать G в терминах некоторых подходящих топологических объектов, ассоциированных с K , описать конечные абелевы расширения K в терминах открытых подгрупп конечного индекса в топологическом объекте, ассоциированном с K. В частности, кто -то хочет установить соответствие один к одному между конечными абелевыми расширениями K и их нормой групп в этом топологическом объекте для K . Этот топологический объект является мультипликативной группой в случае локальных полей с конечным полем вычетов и группой классов идеелей в случае глобальных полей. Конечное абелево расширение, соответствующее открытой подгруппе конечного индекса, называется полем классов для той подгруппы, которая дала название теории.

Основной результат состояний теории поля общего класса , что группа G естественно изоморфна проконечного завершения в C _K , мультипликативной группы локального поля или иделя группы классов глобального поля, по отношению к естественной топологии на C _K связанные с конкретной структурой поля K . Эквивалентно, для любого конечного расширения Галуа L поля K существует изоморфизм ( отображение взаимности Артина )

Гал⁡(LK)ab→CKNLK(CL){\ displaystyle \ operatorname {Gal} (L / K) ^ {\ operatorname {ab}} \ to C_ {K} / N_ {L / K} (C_ {L})}

из абелианизации группы Галуа расширений с фактором класса идели группы K по образу нормы в иделя группы классов L .

Для некоторых небольших полей, таких как поле рациональных чисел или его квадратичные мнимые расширения, существует более подробная, очень явная, но слишком конкретная теория, которая дает больше информации. Например, абелианизированная абсолютная группа Галуа G группы является (естественно изоморфной) бесконечным произведением группы единиц целых p-адических чисел, взятых по всем простым числам p , и соответствующее максимальное абелево расширение рациональных чисел является порожденным полем всеми корнями единства. Это известно как теорема Кронекера – Вебера , первоначально выдвинутая Леопольдом Кронекером.Q{\ displaystyle \ mathbb {Q}}Q{\ displaystyle \ mathbb {Q}} . В этом случае изоморфизм взаимности теории полей классов (или отображение взаимности Артина) также допускает явное описание благодаря теореме Кронекера – Вебера . Однако основные конструкции таких более подробных теорий для полей малых алгебраических чисел не распространяются на общий случай полей алгебраических чисел, и в общей теории полей классов используются различные концептуальные принципы.

Стандартный метод построения гомоморфизма взаимности состоит в том, чтобы сначала построить локальный изоморфизм взаимности от мультипликативной группы пополнения глобального поля до группы Галуа его максимального абелевого расширения (это делается внутри локальной теории полей классов), а затем доказать, что произведение всех таких локальных отображений взаимности, когда они определены на группе иделей глобального поля, тривиально на образе мультипликативной группы глобального поля. Последнее свойство называется глобальным законом взаимности и является далеко идущим обобщением квадратичного закона взаимности Гаусса .

Один из методов построения гомоморфизма взаимности использует формирование классов, которое выводит теорию полей классов из аксиом теории полей классов. Этот вывод является чисто топологическим теоретико-групповым, в то время как для установления аксиом необходимо использовать кольцевую структуру основного поля.

Есть методы, которые используют группы когомологий, в частности группу Брауэра, а есть методы, которые не используют группы когомологий и очень явные и плодотворные для приложений.

Возможная теория

Период, термин «теория потенциала»возникает из-за того, что в физике XIX века фундаментальные силы природы считались производными от скалярные потенциалы который удовлетворил Уравнение Лапласа. Пуассон обратился к вопросу об устойчивости планетарного орбиты, которое уже было решено Лагранжем в первой степени приближения из сил возмущения, и вывел Уравнение Пуассона, названный в его честь. Общий вид этого уравнения:

∇2ϕ=σ{ Displaystyle nabla ^ {2} phi = sigma}

где σ — функция источника (как плотность, величина на единицу объема), а φ — скалярный потенциал, который необходимо найти.

В ньютоновской гравитации; массы являются источниками поля, так что силовые линии заканчиваются на объектах, имеющих массу. Точно так же заряды являются источниками и приемниками электростатических полей: положительные заряды испускают силовые линии электрического поля, а силовые линии заканчиваются отрицательными зарядами. Эти концепции поля также проиллюстрированы в общих теорема расходимости, в частности, закон Гаусса для гравитации и электричества. Для случаев не зависящей от времени гравитации и электромагнетизма поля представляют собой градиенты соответствующих потенциалов

г=−∇ϕг,E=−∇ϕе{ Displaystyle mathbf {g} = — nabla phi _ {g} ,, quad mathbf {E} = — nabla phi _ {e}}

поэтому подставляя их в закон Гаусса для каждого случая, получаем

∇2ϕ=4πгρг,∇2ϕ=−ρеϵ{ displaystyle nabla ^ {2} phi = 4 pi G rho _ {g} ,, quad nabla ^ {2} phi = — { rho _ {e} over epsilon _ { 0}}}

где ρ_г это плотность вещества и ρ_е то плотность заряда.

Между прочим, это сходство проистекает из сходства между Закон всемирного тяготения Ньютона и Закон Кулона.

В случае отсутствия источника (например, вакуума или парных зарядов) эти потенциалы подчиняются Уравнение Лапласа:

∇2ϕ={ displaystyle nabla ^ {2} phi = 0}

Для распределения массы (или заряда) потенциал можно разложить в ряд сферические гармоники, а п-й член в ряду можно рассматривать как потенциал, возникающий из 2п-моменты (см. мультипольное расширение). Для многих целей в расчетах нужны только члены монополя, диполя и квадруполя.

Релятивистская теория поля

Современные формулировки классических теорий поля обычно требуют Ковариация Лоренца поскольку это теперь признано фундаментальным аспектом природы. Теория поля обычно выражается математически с помощью Лагранжианы. Это функция, которая при воздействии принцип действия, порождает уравнения поля и закон сохранения для теории. В действие является скаляром Лоренца, из которого легко выводятся уравнения поля и симметрии.

Повсюду мы используем такие единицы, что скорость света в вакууме равна 1, т.е. c = 1.

Лагранжева динамика

Учитывая тензор поля φ, скаляр, называемый Плотность лагранжиана

L(ϕ,∂ϕ,∂∂ϕ,…,Икс){ displaystyle { mathcal {L}} ( phi, partial phi, partial partial phi, ldots, x)}

может быть построен из φ и его производные.

Из этой плотности можно построить функционал действия путем интегрирования по пространству-времени,

S=∫L−гd4Икс.{ displaystyle { mathcal {S}} = int {{ mathcal {L}} { sqrt {-g}} , mathrm {d} ^ {4} x}.}

куда −гd4Икс{ displaystyle { sqrt {-g}} , mathrm {d} ^ {4} x} форма объема в искривленном пространстве-времени. (г≡Det(гμν)){ Displaystyle (г экв { текст {det}} (г _ { му ню}))}

Следовательно, сам лагранжиан равен интегралу плотности лагранжиана по всему пространству.

Затем, применяя принцип действия, уравнения Эйлера – Лагранжа получаются

δSδϕ=∂L∂ϕ−∂μ(∂L∂(∂μϕ))+⋯+(−1)м∂μ1∂μ2⋯∂μм−1∂μм(∂L∂(∂μ1∂μ2⋯∂μм−1∂μмϕ))={ displaystyle { frac { delta { mathcal {S}}} { delta phi}} = { frac { partial { mathcal {L}}} { partial phi}} — partial _ { mu} left ({ frac { partial { mathcal {L}}} { partial ( partial _ { mu} phi)}} right) + cdots + (- 1) ^ { m} partial _ { mu _ {1}} partial _ { mu _ {2}} cdots partial _ { mu _ {m-1}} partial _ { mu _ {m}} left ({ frac { partial { mathcal {L}}} { partial ( partial _ { mu _ {1}} partial _ { mu _ {2}} cdots partial _ { mu _ {m-1}} partial _ { mu _ {m}} phi)}} right) = 0.}

Векторное поле градиентов

В каких отношениях вы находитесь с производной по направлению и градиентом? …ничего страшного, от ненависти до любви – один шаг =) Напоминаю, что градиент функции в точке – это несвободный вектор, указывающий направление максимального роста функции в данной точке и определяющий скорость этого роста.

Нахождение векторной функции градиентов – есть популярный и распространённый способ получить из скалярного поля поле векторное. При условии существования соответствующих частных производных функции двух и трёх переменных:

Смысл очень прост. Так, если функция задаёт скалярное поле глубины озера, то соответствующая векторная функция определяет множество несвободных векторов, каждый из которых указывает направление наискорейшего подъёма дна в той или иной точке и скорость этого подъёма.

Если функция задаёт скалярное поле температуры некоторой области пространства, то соответствующее векторное поле характеризует направление и скорость наибыстрейшего прогревания пространства в каждой точке этой области.

Разберём общую математическую задачу:

Пример 3

Дано скалярное поле и точка . Требуется:

1) составить градиентную функцию скалярного поля;

2) найти градиент поля в точке и вычислить его длину;

3) вычислить производную по направлению нормального вектора к поверхности в точке , образующего с положительной полуосью тупой угол.

Непосредственно к решению задачи это не относится, но сразу обратим внимание, что скалярное поле не определено на всех трёх координатных плоскостях. 1) Быстренько вспоминаем, как находить частные производные функции трёх переменных:

1) Быстренько вспоминаем, как находить частные производные функции трёх переменных: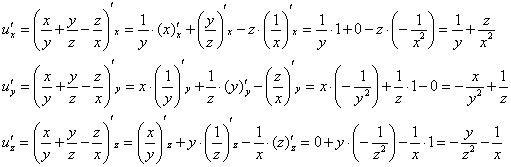

Составим функцию, которая определяет векторное поле градиентов:

И ещё раз – в чём её смысл? Полученная векторная функция каждой точке области определения скалярного поля ставит в соответствие вектор , указывающий направление и максимальную скорость роста функции в данной точке.

И один из таких векторов нам предстоит найти в следующем пункте:

2) Вычислим частные производные в точке :

Таким образом:– ещё раз подчёркиваю, что этот вектор исходит из точки , и перемещать его никуда нельзя! По той причине, что он характеризует направление наискорейшего возрастания функции именно в точке «эм нулевое», а не где-то ещё!

Мерилом же этой максимальной скорости как раз является длина градиента:

3) Вычислим производную по направлению нормального вектора к поверхности в точке , образующего с положительной полуосью тупой угол.

Немного мудрёно, но разобраться немудренО. Во-первых, убедимся, что точка «эм нулевое» действительно принадлежит данной поверхности:
Получено верное равенство. ОК.

Что это за поверхность – нас не интересует, нам важен её нормальный вектор в точке , да не абы какой, а образующий с полуосью тупой угол.

Вспоминаем материал ещё одного урока: вектор нормали к поверхности в точке задаётся следующим образом:

В данном случае:

Но нужный ли это вектор? Как выяснить угол, который он образует с полуосью ? …Сегодня у нас какой-то экскурс в фильмы… =) и сейчас на очереди фильм «Вспомнить всё». Вычислим скалярное произведение вектора с направляющим вектором положительной «зетовой» полуоси:

, следовательно, угол между этими векторами острый, что нас не устраивает!

И поэтому нужно выбрать противоположно направленный нормальный вектор:

Заметим заодно, что нормальные векторы в отличие от градиентов – свободны, их задача лишь указать направление.

Вычислим направляющие косинусы данного направления, или, что то же самое – координаты единичного вектора, сонаправленного с вектором :

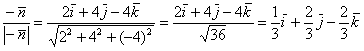
Контроль: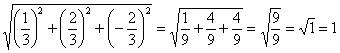

Таким образом, искомая производная по направлению: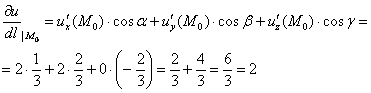

Напоминаю, что это значение характеризует скорость роста функции в точке по направлению вектора , и оно не может оказаться больше, чем (максимальной скорости роста в данной точке).

Ответ: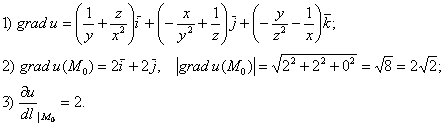

Небольшой пример для самостоятельного решения:

Пример 4

Найти угол между градиентами скалярных полей и в точке

Просто и со вкусом. …Как найти угол? – с помощью того же скалярного произведения. Ну и, очевидно, тут придётся «тряхнуть» многоэтажными дробями и некоторой тригонометрией. Краткое решение и ответ в конце урока.

Что делать, если вам предложено «плоское» скалярное поле ? Просто убавьте одну координату, соответствующие примеры можно найти в статье Производная по направлению и градиент функции. По существу, мы вновь прорешали примеры той статьи, только немного в другой интерпретации.

Ссылки [ править ]

Артин, Эмиль ; Тейт, Джон (1990), Теория поля классов , Редвуд-Сити, Калифорния: Addison-Wesley, ISBN 978-0-201-51011-9
Cassels, JWS ; Фрёлих, Альбрехт , ред. (1967), алгебраическая теория чисел , Academic Press , Zbl 0153.07403
Конрад, Кейт , История теории поля классов.
Фесенко, Иван Б ; Востоков, Сергей В. (2002), Локальные поля и их расширения , Переводы математических монографий, 121 (второе изд.), Провиденс, Род-Айленд: Американское математическое общество , ISBN 978-0-8218-3259-2, MR 1915966
Гра, Жорж (2005), Теория поля классов: от теории к практике (исправленное 2-е издание), Монографии Springer по математике, xiii + 507 страниц , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-44133-5
Ивасава, Кенкичи (1986), Теория поля локальных классов , Оксфордские математические монографии, The Clarendon Press Oxford University Press, ISBN 978-0-19-504030-2, Руководство по ремонту 0863740 , Zbl 0604.12014
Кавада, Юкиёси (1955), «Классовые образования», Duke Math. J. , 22 : 165-177, DOI : 10,1215 / s0012-7094-55-02217-1 , Zbl +0067,01904
Кавада, Юкиёси; Satake, I. (1956), «Классовые образования. II», J.Fac. Наук. Tokyo Sect. 1А , 7 : 353–389, Zbl 0101.02902
Нойкирх, Юрген (1986), Теория поля классов , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-15251-4
Нойкирх, Юрген (1999). Алгебраическая теория чисел . Grundlehren der Mathematischen Wissenschaften . 322 . Берлин: Springer-Verlag. ISBN 978-3-540-65399-8. Руководство по ремонту 1697859 . Zbl 0956.11021 .

Авторитетный контроль	MA : 195831351 NDL : 00569797

Предпосылки теории поля: исторический контекст и гештальт

Курт Левин (1890-1947) родился в Могильно, немецком городе, который сейчас является частью Польши..

Его академическая работа началась в Берлинском университете после того, как он был солдатом Первой мировой войны. Там он работал в лаборатории вместе с создателями гештальт-школы: Вертхаймером, Келером и Коффкой..

Психологи этой школы оспаривали доминирующую парадигму времени и утверждали, что для понимания поведения важны не только сами стимулы, но и то, как индивидуум воспринимает эти стимулы.

Для них целое было чем-то большим, чем сумма его частей, и внутри этого целого субъективный опыт был также неотделимой частью.

Будучи евреем, приход к власти нацистской партии был угрозой, которая привела его к эмиграции в Соединенные Штаты в 1933 году, где он продолжит свою академическую работу.

Для Левина теория Гештальта была бы основой, на которой он разработал бы свою теорию поля. Точно так же его опыт работы в качестве беженца повлиял на его работу из-за его заботы о социальной борьбе, политике и о том, как влиять на поведение групп..

Работа людей и групп

Левин представляет свою теорию как объяснение индивидуальной психологии личности, но в конечном итоге приводит к анализу групп.

Одним из великих вкладов Левина является то, что он начал с гештальт-психологии, чтобы определить группы в целом, систему, которую можно изучать как основную единицу анализа..

Фундаментальный аспект группы заключается в том, что существует взаимозависимость, поскольку группы возникают из-за стремления отдельных лиц объединяться для удовлетворения своих потребностей..

В этом аспекте социальное поле относится к группе сил, которым подвергается группа.

Баланс в системах

Системы (люди или группы) находятся под влиянием различных сил, которые находятся в баланс. Находясь в постоянном изменении и взаимодействии, система постоянно находится под влиянием внутренних и внешних факторов, которые могут привести к потере этого баланса.

В случае групп считается, что баланс находится между потребностями группы и потребностями индивида, где обе крайности (индивидуализм или поглощение индивида группой) были бы нежелательны..

Эта потеря баланса, групповая или индивидуальная, вызывает напряженность в системе и вызывает действие или движение (которое он называет передвижение) который стремится восстановить этот баланс и снять напряжение.

Будут компоненты, которые снимают напряжение (с Валенсия положительные) и объекты, которые препятствуют снижению напряжения (с отрицательной валентностью).

Левин и его ученик Зейгарник (1927) продемонстрировали влияние стресса на память о задачах / ситуациях, так как задачи, вызывающие напряжение, легче запомнить позже.

Происхождение конфликтов

Когда в игру вступают несколько сил, могут возникнуть конфликты. Левин определил конфликт как противостояние валентных сил одинаковой интенсивности.

Конфликты могут быть трех типов:

Подход / приближение: когда нужно выбирать между двумя товарами, то есть двумя объектами положительной валентности.
Избегание / избегание: когда нужно выбирать между двумя пороками, то есть двумя объектами с отрицательной валентностью.
Подход / избегание: когда сталкиваешься с объектом, который имеет положительную и отрицательную валентность одновременно. Например, когда вы хотите что-то, но это требует много усилий (Sánchez, 2014).

Все эти концепции также помогают понять, как они могут быть созданы изменения в группах. По словам Левина, поскольку индивид не может быть отделен от группы, изменения должны начаться на уровне группы (стандарты, нормы и т. Д.), Чтобы уменьшить сопротивление индивидов..

Значимость теории поля Курта Левина

Теория Левина – одна из тех, что оживили представление об индивиде как сложном энергетическом поле, мотивируемом психологическими силами и ведущем себя избирательно и творчески. Человек-пустышка наполнился психологическими потребностями, намерениями, надеждами, притязаниями. Робот превратился в живого человека.

Грубый и скучный материализм уступил место более гуманистическому взгляду на человека. В то время как «объективная» психология проверяла многие свои эмпирические положения на собаках, кошках и крысах, теория Левина вела к исследованию человеческого поведения в более или менее естественной обстановке.

Дети в игре, подростки в групповой активности, рабочие на фабриках, люди, планирующие расход пищи, вот некоторые из естественных жизненных ситуаций, в которых эмпирически проверялись гипотезы, выведенные из теории Левина. Жизненность исследований, убедительность теории поля – неудивительно, что точка зрения Левина стала широко популярной.

сила теории, независимо от ее формальной адекватности или претензии быть математической моделью, оправдывает высокую оценку теории Левина в современной психологии. «Основные представления Левина… изобилуют скрытыми неистощимыми смыслами, и это – гарантия дальнейшего развития» (Heider, 1959, с. 119). Оценка теории поля Хайдером остается валидной и теперь. Левиновская теория человека в среде все еще очень жизненна.

Бихевиоризм (англ. behavior — поведение) — это систематический подход к изучению поведения людей и других животных. Он предполагает, что все поведение состоит из рефлексов, реакций на определенные стимулы в среде, а также последствий индивидуальной истории, таких как подкрепление и наказание, совместно с настоящим мотивационным состоянием индивида и контролирующими стимулами.
Эвристи́ческий — происходит от сущ. эвристика, далее из лат. heuristica из др.-греч. εὑρετικός «находчивый», далее из εὑρίσκω «находить, обнаруживать», далее из праиндоевр. *were- «найти». Cвязанный, соотносящийся по значению с существительным эвристика; такой, который помогает находить, обнаруживать что-либо/

Эвристический алгоритм (эвристика) — алгоритм решения задачи, включающий практический метод, не являющийся гарантированно точным или оптимальным, но достаточный для решения поставленной задачи. Позволяет ускорить решение задачи в тех случаях, когда точное решение не может быть найдено.

Источинки информации:

Википедия — , Полевое поведение
Psyera.ru — Теория поля немецкого психолога Курта Левина
C.S.Hall, G.Lindsey (Келвин С. Холл , Гарднер Линдсей)Теория Личности (Theories of Personality): Глава 9. Теория поля Курта Левина
Перевод И.Б.Гриншпун

Если у вас есть какие-либо интересные дополнения, либо ссылки на материалы по теме, вы можете поделиться в форме ниже.

Попытки объединения

Попытки создать единую теорию поля на основе классической физики являются классическими едиными теориями поля. В период между двумя мировыми войнами идея объединения гравитации с электромагнетизмом активно развивалась несколькими математиками и физиками, такими как Альберт Эйнштейн , Теодор Калуца , Герман Вейль , Артур Эддингтон , Густав Ми и Эрнст Райхенбахер.

Ранние попытки создать такую теорию были основаны на включении электромагнитных полей в геометрию общей теории относительности . В 1918 году случай первой геометризации электромагнитного поля был предложен в 1918 году Германом Вейлем. В 1919 году идею пятимерного подхода предложил Теодор Калуца . На основе этого была разработана теория под названием теория Калуцы-Клейна . Он пытается объединить гравитацию и электромагнетизм в пятимерном пространстве-времени . Есть несколько способов расширить репрезентативную основу единой теории поля, которые были рассмотрены Эйнштейном и другими исследователями. Эти расширения в целом основаны на двух вариантах. Первый вариант основан на ослаблении условий, наложенных на исходную формулировку, а второй основан на введении в теорию других математических объектов. Примером первого варианта является ослабление ограничений четырехмерного пространства-времени путем рассмотрения многомерных представлений. Это используется в теории Калуцы-Клейна . Что касается второго, наиболее ярким примером является концепция аффинной связи, которая была введена в общую теорию относительности в основном благодаря работам Туллио Леви-Чивиты и Германа Вейля .

Дальнейшее развитие квантовой теории поля сместило фокус поиска единой теории поля с классического на квантовое описание. Из-за этого многие физики-теоретики отказались от поиска классической единой теории поля. Квантовая теория поля будет включать объединение двух других фундаментальных сил природы , сильной и слабой ядерной силы, которые действуют на субатомном уровне.