Роль импульса и кинетической энергии в описании движения
Различие между величинами \(~\vec p\) и Ek не ограничивается тем, что одна из них векторная, а другая скалярная.
Из равенства (1) видно, что если сила \(~\vec F\) задана, изменение импульса определяется только временем действия силы и не зависит от того, к какому телу она приложена. Любое тело (тело любой массы) под действием данной силы за данное время изменит свой импульс на одну и ту же величину. Даже если бы, например, столкнулись герои басни Крылова «Слон и Моська», то импульс каждого из них изменился бы одинаково.
Равенство (2) говорит о том, что при заданной силе изменение кинетической энергии тела определяется только расстоянием, пройденным телом в направлении действия силы (произведение s cos α — это проекция перемещения на направление силы). Любое тело под действием данной силы на данном расстоянии изменит свою кинетическую энергию на одну и ту же величину.
Таким образом, изменение импульса связано с промежутком времени, необходимым для изменения скорости тела, а изменение кинетической энергии связано с расстоянием, которое тело должно пройти для изменения его скорости (разумеется, при заданной силе).
Другими словами, изменение импульса — это характеристика действия силы — во времени, а изменение кинетической энергии — характеристика действия силы в пространстве.
Откуда появился термин «импульс»
За несколько веков до того, как в физике появилось понятие количества механического движения тела, считалось, что причиной любого перемещения в пространстве является особая сила — импетус.
В 14 веке в это понятие внес коррективы Жан Буридан. Он предположил, что летящий булыжник обладает импетусом, прямо пропорциональным скорости, который был бы неизменным, если бы отсутствовало сопротивления воздуха. В то же время, по мнению этого философа, тела с большим весом обладали способностью «вмещать» больше такой движущей силы.
Дальнейшее развитие понятию, позднее названного импульсом, дал Рене Декарт, который обозначил его словами «количество движения». Однако он не учитывал, что скорость имеет направление. Именно поэтому выдвинутая им теория в некоторых случаях противоречила опыту и не нашла признания.

О том, что количество движения должно иметь еще и направление, первым догадался английский ученый Джон Валлис. Произошло это в 1668 году. Однако понадобилась еще пара лет, чтобы он сформулировал известный закон сохранения количества движения. Теоретическое доказательство этого факта, установленного эмпирическим путем, было дано Исааком Ньютоном, который использовал открытые им же третий и второй законы классической механики, названные его именем.
Основные теоретические сведения
Импульс тела
Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р. Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:
Направление вектора импульса совпадает с направлением вектора скорости тела (направлен по касательной к траектории). Единица измерения импульса – кг∙м/с.
Изменение импульса одного тела находится по формуле (обратите внимание, что разность конечного и начального импульсов векторная):
где: pн – импульс тела в начальный момент времени, pк – в конечный. Главное не путать два последних понятия.
Абсолютно упругий удар – абстрактная модель соударения, при которой не учитываются потери энергии на трение, деформацию, и т.п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется. Может поменяться только его направление. При этом угол падения равен углу отражения.
Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Например, пластилиновый шарик при падении на любую поверхность полностью прекращает свое движение, при столкновении двух вагонов срабатывает автосцепка и они так же продолжают двигаться дальше вместе.
Закон сохранения импульса
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения импульса (ЗСИ). Следствием его являются законы Ньютона. Второй закон Ньютона в импульсной форме может быть записан следующим образом:
Как следует из данной формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Аналогично можно рассуждать для равенства нулю проекции силы на выбранную ось. Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Аналогичные записи можно составить и для остальных координатных осей. Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.
Сохранение проекции импульса
Возможны ситуации, когда закон сохранения импульса выполняется только частично, то есть только при проектировании на одну ось. Если на тело действует сила, то его импульс не сохраняется. Но всегда можно выбрать ось так, чтобы проекция силы на эту ось равнялась нулю. Тогда проекция импульса на эту ось будет сохраняться. Как правило, эта ось выбирается вдоль поверхности по которой движется тело.
Многомерный случай ЗСИ. Векторный метод
В случаях если тела движутся не вдоль одной прямой, то в общем случае, для того чтобы применить закон сохранения импульса, нужно расписать его по всем координатным осям, участвующим в задаче. Но решение подобной задачи можно сильно упростить, если использовать векторный метод. Он применяется если одно из тел покоится до или после удара. Тогда закон сохранения импульса записывается одним из следующих способов:
В этих формулах буквой υ обозначены скорости тел до соударения, а буквой u обозначены скорости тел после соударения. Из правил сложения векторов следует, что три вектора в этих формулах должны образовывать треугольник. Для треугольников применяется теорема косинусов. Если правильно записать соответствующую теорему косинусов, то зачастую получается уравнение из которого можно найти нужную величину. Однако, иногда к правильно записанной теореме косинусов еще нужно будет добавить правильно записанный закон сохранения энергии (смотрите следующий раздел). В этом случае получится система уравнений из которых наверняка можно будет найти нужную величину.
1.16. Импульс тела window.top.document.title = «1.16. Импульс тела»;
Пусть на тело массой m в течение некоторого малого промежутка времени Δt действовала сила Под действием этой силы скорость тела изменилась на Следовательно, в течение времени Δt тело двигалось с ускорением
Из основного закона динамики (второго закона Ньютона) следует:
Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения). Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с).
Физическая величина, равная произведению силы на время ее действия, называется импульсом силы. Импульс силы также является векторной величиной.
В новых терминах второй закон Ньютона может быть сформулирован следующим образом: изменение импульса тела (количества движения) равно импульсу силы.
Обозначив импульс тела буквой второй закон Ньютона можно записать в виде
Именно в таком общем виде сформулировал второй закон сам Ньютон. Сила в этом выражении представляет собой равнодействующую всех сил, приложенных к телу. Это векторное равенство может быть записано в проекциях на координатные оси:
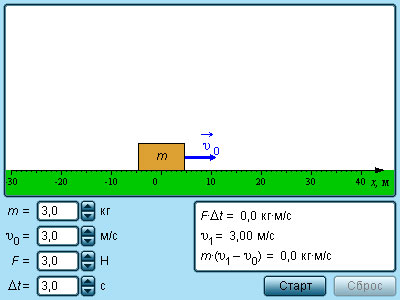 |
|
Модель. Импульс тела |
Таким образом, изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось. Рассмотрим в качестве примера одномерное движение, т. е. движение тела по одной из координатных осей (например, оси OY). Пусть тело свободно падает с начальной скоростью υ под действием силы тяжести; время падения равно t. Направим ось OY вертикально вниз. Импульс силы тяжести Fт = mg за время t равен mgt. Этот импульс равен изменению импульса тела
Этот простой результат совпадает с кинематической формулой для скорости равноускоренного движения. В этом примере сила оставалась неизменной по модулю на всем интервале времени t. Если сила изменяется по величине, то в выражение для импульса силы нужно подставлять среднее значение силы Fср на промежутке времени ее действия. Рис. 1.16.1 иллюстрирует метод определения импульса силы, зависящей от времени.
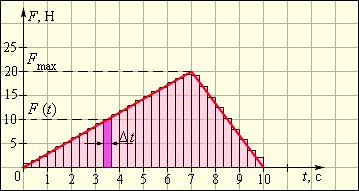 |
| Рисунок 1.16.1.Вычисление импульса силы по графику зависимости F(t) |
Выберем на оси времени малый интервал Δt, в течение которого сила F (t) остается практически неизменной. Импульс силы F (t) Δt за время Δt будет равен площади заштрихованного столбика. Если всю ось времени на интервале от до t разбить на малые интервалы Δti, а затем просуммировать импульсы силы на всех интервалах Δti, то суммарный импульс силы окажется равным площади, которую образует ступенчатая кривая с осью времени. В пределе (Δti → 0) эта площадь равна площади, ограниченной графиком F (t) и осью t. Этот метод определения импульса силы по графику F (t) является общим и применим для любых законов изменения силы со временем. Математически задача сводится к интегрированию функции F (t) на интервале .
Импульс силы, график которой представлен на рис. 1.16.1, на интервале от t1 = 0 с до t2 = 10 с равен:
В этом простом примере
В некоторых случаях среднюю силу Fср можно определить, если известно время ее действия и сообщенный телу импульс. Например, сильный удар футболиста по мячу массой 0,415 кг может сообщить ему скорость υ = 30 м/с. Время удара приблизительно равно 8·10–3 с.
Импульс p, приобретенный мячом в результате удара есть:
Следовательно, средняя сила Fср, с которой нога футболиста действовала на мяч во время удара, есть:
Это очень большая сила. Она приблизительно равна весу тела массой 160 кг.
Если движение тела во время действия силы происходило по некоторой криволинейной траектории, то начальный и конечный импульсы тела могут отличаться не только по модулю, но и по направлению. В этом случае для определения изменения импульса удобно использовать диаграмму импульсов, на которой изображаются вектора и , а также вектор построенный по правилу параллелограмма. В качестве примера на рис. 1.16.2 изображена диаграмма импульсов для мяча, отскакивающего от шероховатой стенки. Мяч массой m налетел на стенку со скоростью под углом α к нормали (ось OX) и отскочил от нее со скоростью под углом β. Во время контакта со стеной на мяч действовала некоторая сила направление которой совпадает с направлением вектора
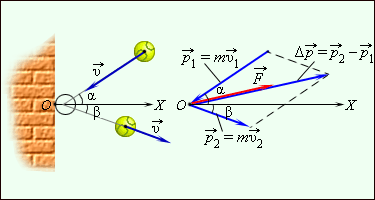 |
| Рисунок 1.16.2.Отскок мяча от шероховатой стенки и диаграмма импульсов |
При нормальном падении мяча массой m на упругую стенку со скоростью после отскока мяч будет иметь скорость Следовательно, изменение импульса мяча за время отскока равно В проекциях на ось OX этот результат можно записать в скалярной форме Δpx = –2mυx. Ось OX направлена от стенки (как на рис. 1.16.2), поэтому υx < 0 и Δpx > 0. Следовательно, модуль Δp изменения импульса связан с модулем υ скорости мяча соотношением Δp = 2mυ.
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
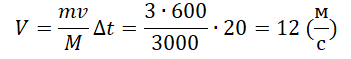
Направления работы
Метод Томатис
Метод «Томатис» используется как при многих патологических состояниях (ЗПР, ЗРР, ЗПРР, ОНР, СДВГ, ДЦП, УО, РАС, РДА), так и для совершенствования навыков, где требуется более тонкое восприятие звуков (изучение иностранных языков и избавление от акцента, постановка голоса и плавность речи), а также для увеличения работоспособности, улучшения памяти, внимания и концентрации и повышения скорости обработки информации.
Сенсорная комната
Сенсорная комната — это комната, оснащенная специальным световым, звуковым и тактильным оборудованием, стимулирующим развитие сенсорной сферы ребенка, мелкой и крупной моторики. Занятия в сенсорной комнате позволяют активировать головной мозг через основные органы чувств (зрение, слух, обоняние, осязание). Сенсорная интеграция необходима как для детей с патологиями, так и для общего развития ребенка.
Школа раннего развития
Школа раннего развития В нашем Центре проводятся специальные занятия по раннему развитию малышей с 2-х месяцев на основе сенсорной гимнастики, т.е. активной стимуляции психического интеллекта. Если ваш ребенок будет посещать Школу раннего развития, то к своему возрасту он будет больше уметь и быстрее соображать, чем его сверстники. С ребенком необходимо правильно заниматься с самого рождения.
Занятия с нейропсихологом
Нейропсихолог – это специалист, работающий с высшими психическими функциями у детей: восприятием, вниманием, памятью, мышлением, речью, поведением. Нейрокоррекция наиболее эффективна в дошкольном и младшем школьном возрасте
Занятия с нейропсихологом показаны при ЗРР, ЗПР, ЗПРР, ОНР, СДВГ, РАС, ММД, дисграфии, а также при плохой успеваемости, заторможенности и быстрой утомляемости.
Мозжечковая стимуляция
Мозжечковая стимуляция – это специальный комплекс занятий, направленный на стимуляцию и нормализацию работы ствола головного мозга и мозжечка. Цель программы – научить мозг правильно обрабатывать информацию, полученную от органов чувств. В нашем Центре занятия проводятся на оригинальном оборудовании Balametrics’
Занятия улучшают речь, память, внимание, поведение, координацию и др
Подготовка к школе
Сейчас к новоиспеченному школьнику предъявляется много требований. И без определенных навыков и умений теперь детям очень трудно усваивать школьный материал. Если ваш ребенок невнимательный и неусидчивый, или же имеет такие диагнозы как СДВГ, дисграфия и дислексия, наша команда специалистов по детскому развитию предложит вам и вашему будущему первокласснику профессиональную помощь.
Занятия с логопедом
Заниматься речевым развитием ребенка необходимо с самого рождения, ведь большинство патологий могут быть выявлены уже на первом году жизни. Если Вы пропустили этот благодарный период, то обратиться за консультацией к логопеду следует хотя бы в 2 года. После проведения диагностики Вам могут быть предложены индивидуальные или групповые занятия с логопедом. Своевременная помощь поможет ребенку избежать задержки речевого развития.
Логопедический массаж
Детям со значительными речевыми расстройствами (при алалии, дизартрии, дислалии, укороченной подъязычной уздечке, нарушении тонуса мышц артикуляционного аппарата, а также при заикании, гнусавости, нарушениях голоса, гиперсаливации) для коррекции звукопроизношения необходимо проводить логопедический массаж. Массаж изменяет состояние мышц, нервов, кровеносных сосудов и тканей периферического речевого аппарата.
Логоритмика
Занятия логоритмикой направлены на развитие чувства ритма, формирование правильного дыхания, развитие артикуляционного аппарата и лицевой мускулатуры, крупной и мелкой моторики.Логоритмика полезна для профилактики задержки речевого развития и для социализации ребенка
Развитие речи в дошкольном возрасте имеет важно для последующей адаптации ребенка к школе, усвоении навыков устной и письменной речи
Мы будем рады, если нашими услугами воспользуются не только жители Реутова, но и ближайших населенных пунктов: Балашиха, Железнодорожный, Купавна, Салтыкова, Электросталь, Кучино, Люберцы, а также соседних с нами районов Москвы — Новокосино, Новогиреево, Ивановское, Вешняки, Выхино, Измайлово, Жулебино, Кузьминки и др.!
В связи с введением онлайн-услуг мы проводим дистанционные консультации и занятия с жителями всех регионов России.
Определение средней силы
Имеются случаи, когда определение средней силы Fсрвозможно при известных времени и данных о сообщенном импульсе. При сильной ударе по мячу с массой ,415 кг можно сообщить скорость, равную v=30 мс. Приблизительным временем удара является значение 8·10–3 с.
Тогда формула импульса приобретает вид:
p=mv=12,5 кг·мс.
Чтобы определить среднюю силу Fсрво время удара, необходимо Fср=p∆t=1,56·103 Н.
Получили очень большое значение, которое равняется телу массой 160 кг.
Когда движение происходит по криволинейной траектории, то начальное значение p1→ и конечноеp2→ могут быть различны по модулю и по направлению. Для определения импульса ∆p→ применяют диаграмму импульсов, где имеются векторы p1→ и p2→, а ∆p→=p2→-p1→ построен по правилу параллелограмма.
Пример 2
Для примера приводится рисунок 1.16.2, где нарисована схема импульсов мяча, отскакивающего от стены. При подаче мяч с массой m со скоростью v1→ налетает на поверхность под углом α к нормали и отскакивает со скоростью v2→ с углом β. При ударе в стену мяч подвергался действию силы F→, направленной также, как и вектор ∆p→.
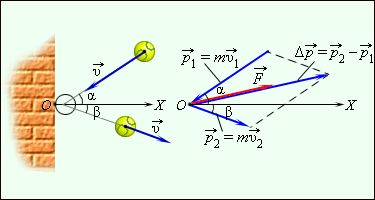
Рисунок 1.16.3. Отскакивание мяча от шероховатой стенки и диаграмма импульсов.
Если происходит нормальное падение мяча с массой m на упругую поверхность со скоростью v1→=v→, тогда при отскоке она изменится на v2→=-v→. Значит, за определенный промежуток времени импульс изменится и будет равен ∆p→=-2mv→. Используя проекции на ОХ, результат запишется как Δpx=–2mvx. Из рисунка 1.16.3 видно, что ось ОХ направлена от стенки, тогда следует vx< и Δpx>. Из формулы получим, что модуль Δp связан с модулем скорости, который принимает вид Δp=2mv.
Всё ещё сложно?
Наши эксперты помогут разобраться
Все услуги
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Главными задачами Центра являются:
- профилактика нарушений развития у детей групп риска;
- социальная реабилитация, адаптация и коррекция отклонений развития;
- психологическая поддержка семей, имеющих ребенка с ограниченными возможностями.
Социальная реабилитация — это мероприятия по восстановлению утраченных ребенком социальных связей и функций, восполнению среды жизнеобеспечения, усилению заботы о нем.
Услуги в Центре оказываются как по запросу (консультации определенных специалистов), так и комплексно (с привлечением специалистов разных направлений).
В Центре используется специальное оборудование, применяются современные новейшие методики. В результате такого подхода эффективность реабилитационных мероприятий увеличивается, процесс восстановления ускоряется (пример: при работе по старым методам восстановление психоречевых функций происходит за 2 года, а при комплексном подключении к процессу социальной реабилитации новых методов, внедренных в центре, эффект наступает в течение 6-9 месяцев).
Импульс — произведение массы на вектор скорости
Импульс или количество движения p объекта определяется как произведение его массы и векторной скорости. Поскольку в этом произведении скорость — векторная величина, импульс также будет вектором, причем направление этого вектора совпадает с направлением вектора скорости:
В системе СИ единица измерения импульса — килограмм-метр в секунду (кг·м/с). Эта единица эквивалентна по размерности единице импульса силы ньютон-секунда (Н·с):
При сравнении импульсов двух объектов нужно сравнить их массы и скорости.
 На двух фотографиях показана одна и та же девочка. На левой фотографии она на большой скорости спускается с горы и её импульс больше, чем на правой фотографии
На двух фотографиях показана одна и та же девочка. На левой фотографии она на большой скорости спускается с горы и её импульс больше, чем на правой фотографии
Сравним, например импульсы одной и той же юной сноубордистки, когда она спускается с горы и поднимается на нее. Хотя это одна и та же девочка с одной и той же массой, ее импульсы в двух показанных на рисунке ситуациях сильно отличаются. Когда она поднимается в гору, ее импульс очень маленький. Зато, когда она быстро спускается с горы, ее импульс в несколько раз больше.
В реальности ни один подвижный объект не имеет постоянного импульса, потому что скорость движения тел редко бывает постоянной. Поэтому обычно правильнее говорить о мгновенном импульсе тела, если можно измерить его мгновенную массу и векторную скорость.
Для примера попробуем подсчитать мгновенный импульс этой девочки, когда она движется вниз в момент, изображенный на левом снимке. Ее масса равна 35 кг, масса доски, одежды и шлема равна 3 кг. Скорость в показанный на левом снимке момент составляет 4 м/с. Движение происходит в направлении на юг. Считаем, что девочка и доска представляют собой одну систему, так как они движутся вместе как одной целое. Считаем также, что эта система также является замкнутой, так как она не теряет массу и на нее не действуют внешние силы. Общая масса системы равна 35 + 3 = 38 кг. Импульс системы направлен в ту же сторону, что и скорость. Поэтому абсолютная величина импульса равна
Таким образом, импульс (количество движения) этой юной сноубордистки равен 152 кг·м/с и направлен на юг. Воспользуемся нашим калькулятором, чтобы преобразовать эту величину в традиционные американские единицы:
Определение через волны де Бройля
В 1924 году была высказана гипотеза о том, что корпускулярно-волновым дуализмом обладают не только фотоны, но и любые другие частицы (протоны, электроны, атомы). Ее автором стал французский ученый Луи де Бройль. Если перевести эту гипотезу на язык математики, то можно утверждать, что с любой частицей, имеющей энергию и импульс, связана волна с частотой и длиной, выражаемыми формулами 11 и 12 соответственно (h — постоянная Планка).
Из последнего соотношения получаем, что модуль импульса и длина волны, обозначаемая буквой «лямбда», обратно пропорциональны друг другу (13).
Если рассматривается частица со сравнительно невысокой энергией, которая движется со скоростью, несоизмеримой со скоростью света, то модуль импульса вычисляется так же, как в классической механике (см. формулу 1). Следовательно, длина волны рассчитывается согласно выражению 14. Иными словами, она обратно пропорциональна произведению массы и скорости частицы, т. е. ее импульсу.

Теперь вы знаете, что импульс тела — это мера механического движения, и познакомились с его свойствами. Среди них в практическом плане особенно важен Закон сохранения. Даже люди, далекие от физики, наблюдают его в повседневной жизни. Например, всем известно, что огнестрельное оружие и артиллерийские орудия дают отдачу при стрельбе. Закон сохранения импульса наглядно демонстрирует и игра в бильярд. С его помощью можно предсказать направления разлета шаров после удара.
Закон нашел применение при расчетах, необходимых для изучения последствий возможных взрывов, в области создания реактивных аппаратов, при проектировании огнестрельного оружия и во многих других сферах жизни.































ЫкщУ